Описание метода ломаных

Выбирем некот т-ку . Построим ф-ю

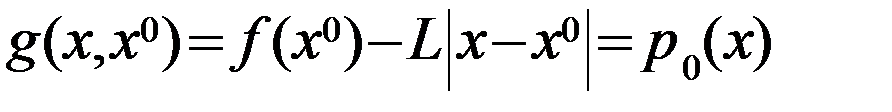и определим 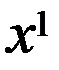из усл. . Очевидно, что x¹=a или x¹=b. Пусть в результате выполнения нескольких шагов определены т-ки х¹,х²,…,хⁿ, n 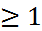. Построим ф-цию g(x,xⁿ)=f(xⁿ)-L|x- xⁿ |.

Строим ф-цию

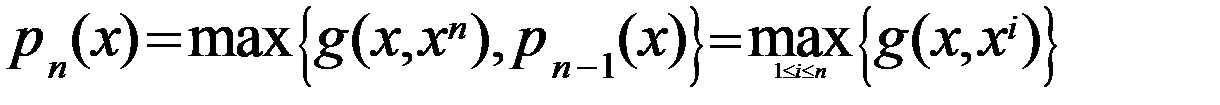Следующее приближение

Процесс вычисл. продолж. до тех пор, пока не будет выполнено нерав-во , где - заданная точность. В кач-ве решения задачи выбирается т-ка .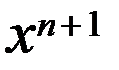

Зам. Метод ломаных сходится при любом начальном при любом начальном приближении.

Зам. Для всех х справедливо соотнош.

т.е. ф-ции р_n(х) приближают ф-цию f(x) снизу, оставаясь каждый раз не выше графика ф-ции f(x).

Зам, Недостаток – с ростом числа шагов растет требуемый объем памяти вычисл машины.

Зам. Для применения метода надо знать константу Липшица.

Теорема. Пусть ф-я уд. усл. Липшица на [a;b], тогда посл-ть полученная методом ломанных такая, что:

1) (1), причем (2)

2) (3)

Док-во. Рассмотрим (4)

(5), 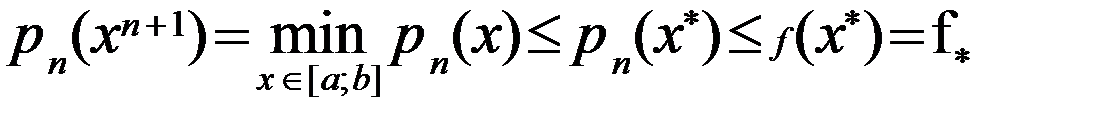(6), где . Из (4)-(6) получаем

т.е. послед-ность явл. возрастающей и ограничена сверху, поэтому . Кроме того, из (4)-(6) следует оценка (2). Покажем, что . Т.к. 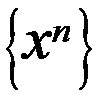ограничена, то из нее можно выделить сходящуюся подпослед-ность . Пусть - некотор. т-ка послед-ности 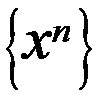. Послед-ность сходится к т-ке при n¹<n²<…<n^k<…

Пример. f(x)=|x²-1|, x [-2,3]. На отр. [-2,3] ф-ция уд. усл. Липшица с константой L₁=4, на отр. [-1,1] L₂=2, на отр. [1,2] L₃=6. На всем отр. L=6. Строим ф-цию g(x,0)=1-6|x|. При x<0, g(x,0)=1+6x, g(-1,0)=-5, x>0, g(x,0)=1-6x, g(1,0)=-5. Т-ка x¹. g(x,3)=8-6|x-3|, g(x,3)=8+6x-18.

Следующ. т-ка x² определ. как min g(x,-2)=3-6|x+2|, g(x,-2)=3-6x-12

Поиск по сайту: