Алгоритм метода скорейшего спуска решения ЗММ

Пусть выбрано некот нач-е приближение и на некоторой итерации построено очередное приближение и вычислены значения , . Рассм.луч, проходящий ч/з т в направлении антиградиента .В этом луче рассм. ф-ю, зависящую от альфа . Рассм. вспомогательную задачу одномерной минимизации (*).

И пусть решение этой задачи достигается в т 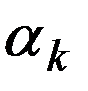: , тогда след. приближение вычисляется по ф-ле .

Итерационный процесс продолжается до тех пор, пока не будет выполнен критерий окончания счета.

В качестве критерия окончания счета могут использоваться нерав-ва:

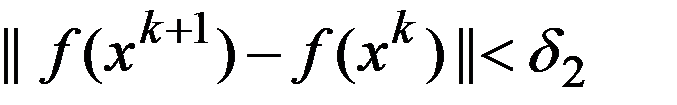; ; , где , , –заданные числа, характеризующие точность счета

Если на некоторой итерации выполняется рав-во , то в т-ке х^k выполн. необход. усл. Оптимальности и итерационный процесс заканчивается.

Если , то сущ.такое неотрицат. , что .

Если значения явл. решением задачи (*), то в этой т-ке должно быть выполнено необходимое усл. оптимальности, т.е.

Вычислим эту производную в т-ке

Получаем, что градиенты, вычисл. в соседних приближениях, постоенных методом скорейшего спуска ортогональны.

Зам. Величину 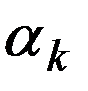можно выбирать из условия , в этом случае метод наз градиентным.

Поиск по сайту: