АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод вариаций Лагранжа

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Пусть в задаче , где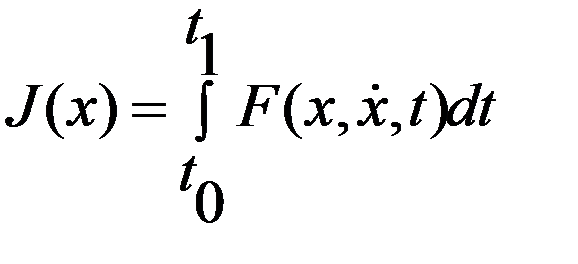

и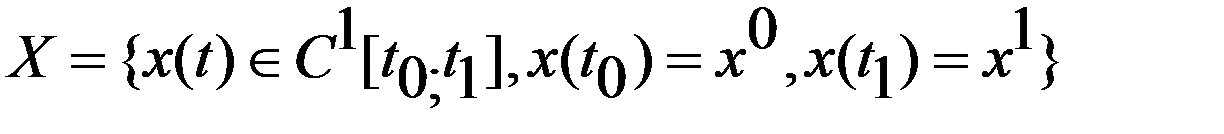

Пусть на кривой дости-тся минимум, тогда все допустимые кривые x(t), из мн-ва X можно представить в виде: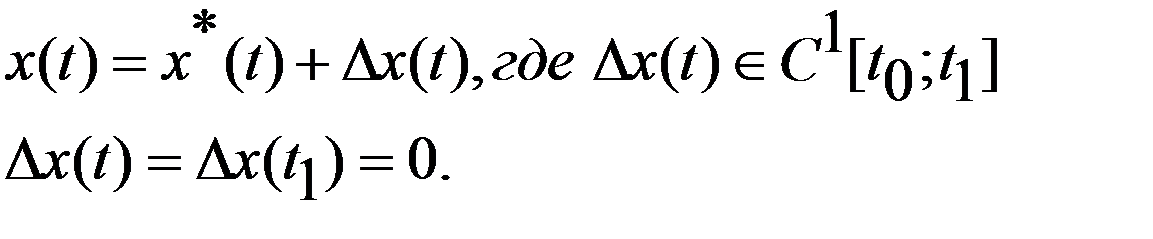

Тогда рассм. приращение функционала:

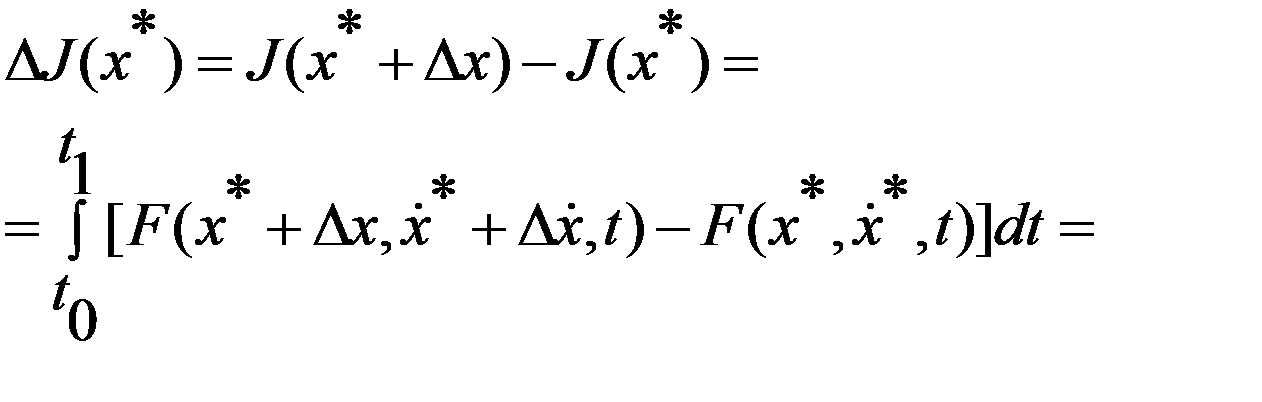
=/ в силу дифференцируемости ф-ции F/=

=

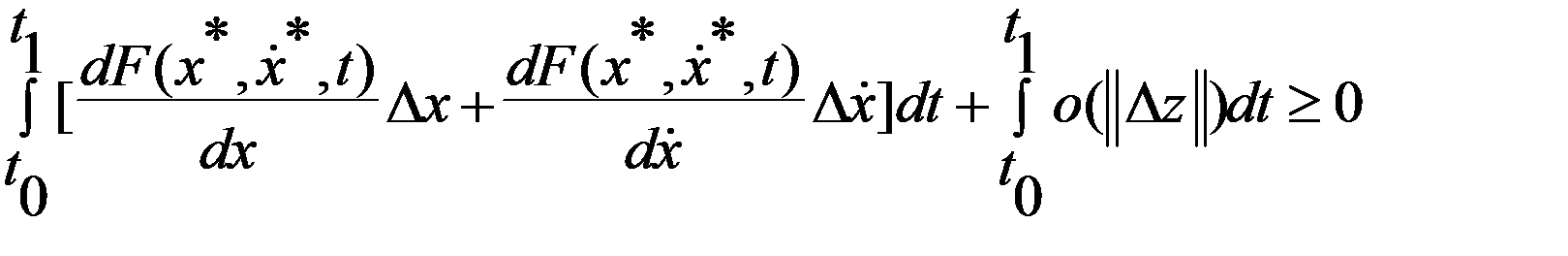
(т.к 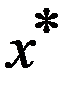минимально), где бесконечно малая велич.

Первый интеграл наз. 1-вой вариацией функционала.

В таком разложении приращения функционала, кривые 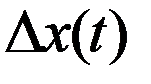имеют произвольную природу, что влечет за собой сложность исследования. Представим кривые 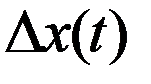в виде однопараметрического семейства ф-ций:

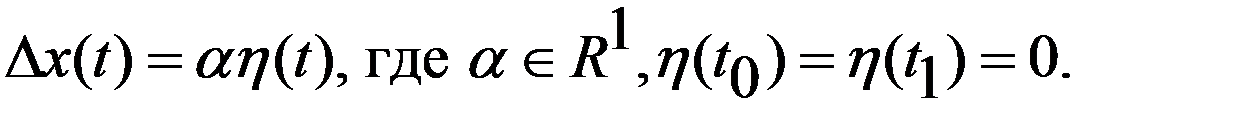
Для таких приращений функций рассмотрим приращение функционала:

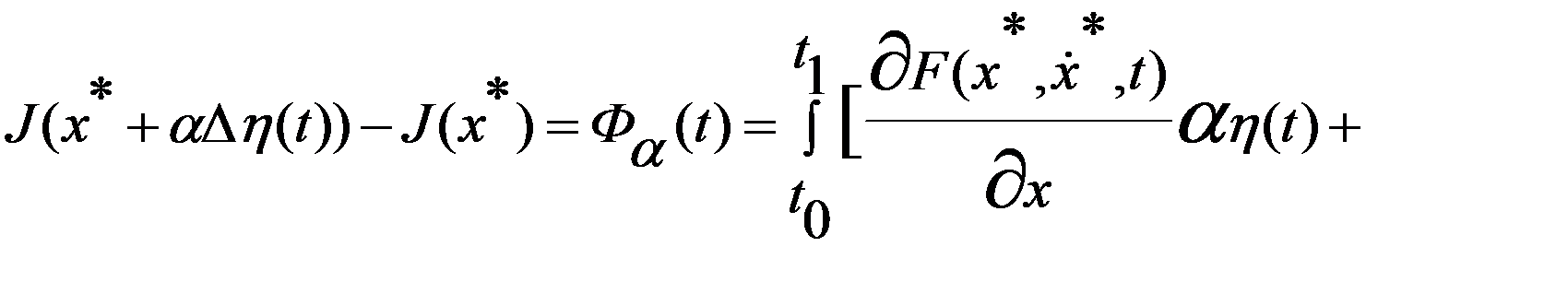
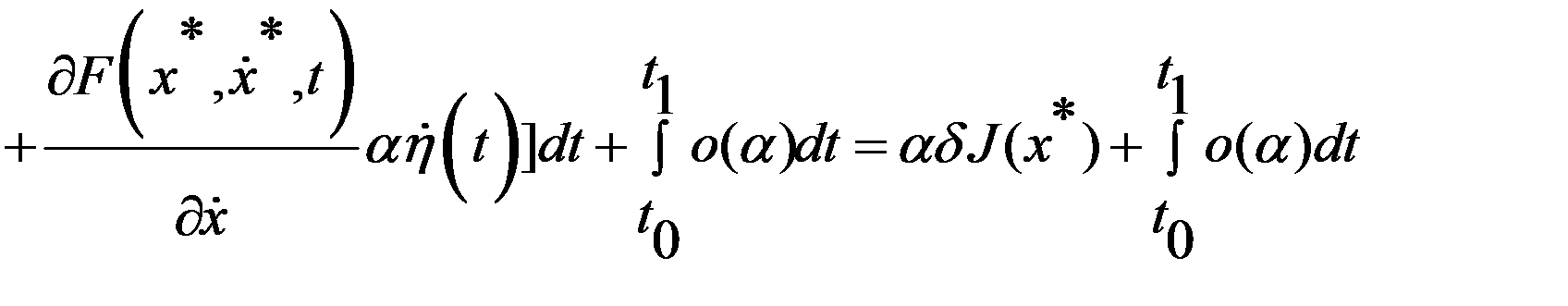
где

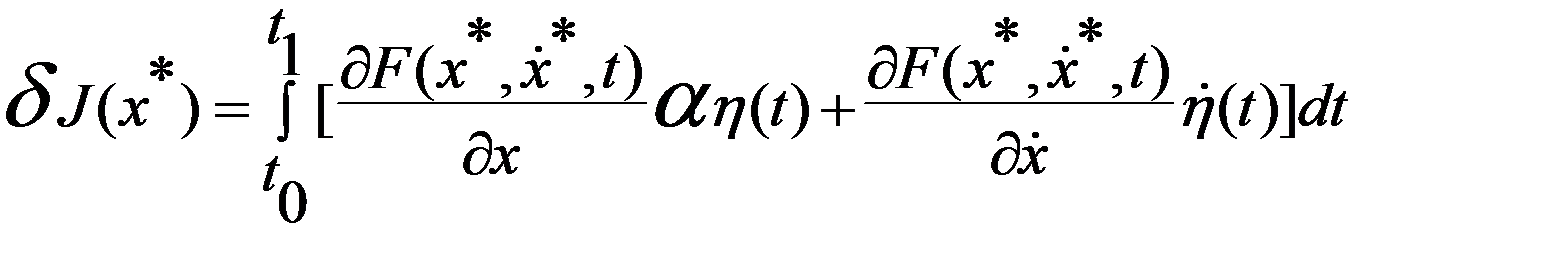
наз. первой вариацией функционала. Т.к

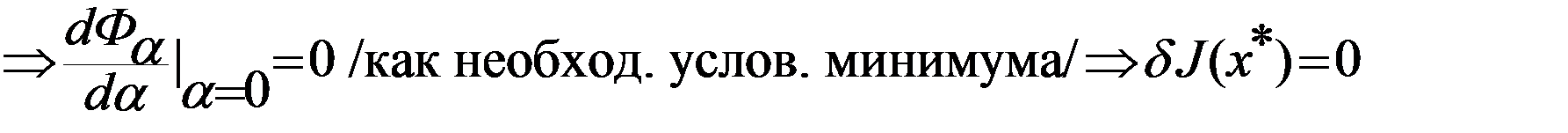
( на кривой подозрительной на минимум)

Замечание: Необходимое условие оптимальности в силу произвольности ф-ций является неудобным для использования на практике.


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)