 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Классический метод решения задачи безусловной минимизации функции многих переменных. Пример
Под кл. методом подразум. подход к поиску точек экстремума ф-ций многих переменных, кот. основан на дифференц. исчислении.
Т1 Вейерштрасса( о достижении верхней и нижней граней непрер. ф-ции., опред-й на огранич. замкнут.мн-ве). Пусть в задаче  мн-во
мн-во  , ограничен-е, замкнутое, а ф-ция
, ограничен-е, замкнутое, а ф-ция  определена, конечна и непр-на на X. Тогда
определена, конечна и непр-на на X. Тогда 
След. Пусть X - замкнуто,  непреп. на X и сущ. Точка
непреп. на X и сущ. Точка 
 ,такая, что мн-во
,такая, что мн-во 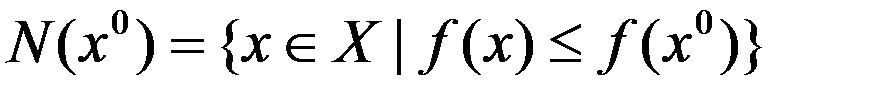
 ограничено.Тогда
ограничено.Тогда  .
.
Т-ма2. Пусть ф-ция  диф-ма в точке
диф-ма в точке  . Если y есть точка лок-го минимума ф-ции
. Если y есть точка лок-го минимума ф-ции  ,то выполн. усл.стационарности
,то выполн. усл.стационарности 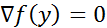 . Д-во. Возьмем произв. точку
. Д-во. Возьмем произв. точку  и построим приращение аргумента
и построим приращение аргумента  где
где 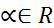 . Рассм. Приращ. ф-ции в точке y, которое разложим на основании опред.диф.ф-ции
. Рассм. Приращ. ф-ции в точке y, которое разложим на основании опред.диф.ф-ции  Разделим последнее равенство на
Разделим последнее равенство на  и устремим
и устремим  к нулю. В пределе получим нерав-во
к нулю. В пределе получим нерав-во  В соотн.(3) положим
В соотн.(3) положим  из чего получим нерав-во
из чего получим нерав-во  котрое может выпол. Только при усл.
котрое может выпол. Только при усл. 
Зам1. Точки  , для кот. выпол. Рав-во
, для кот. выпол. Рав-во 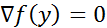 , наз. стационарными. Поиск точек минимума можно начинать с реш-я системы n ур-ний с n неизв-ми величинами
, наз. стационарными. Поиск точек минимума можно начинать с реш-я системы n ур-ний с n неизв-ми величинами  Зам2. Не всякая стац. точка явл. точкой лок. экстр. Пример1. Исслед. на экстр. ф-ю двух переменных
Зам2. Не всякая стац. точка явл. точкой лок. экстр. Пример1. Исслед. на экстр. ф-ю двух переменных  . Р-е. Выч. градиент данной ф-и
. Р-е. Выч. градиент данной ф-и  Из усл. стац. получаем одну точку (0,0), подозрит. на экстр. Знач. ф-и в стац. т-ке равно нулю:
Из усл. стац. получаем одну точку (0,0), подозрит. на экстр. Знач. ф-и в стац. т-ке равно нулю:  .Но
.Но  из чего след., что т-ка (0,0) эктр. не явл. Т-ма3. Пусть ф-ция
из чего след., что т-ка (0,0) эктр. не явл. Т-ма3. Пусть ф-ция  дважды диф-ма в точке
дважды диф-ма в точке  . Если у есть точка лок. миним. зад. (1),то матрица
. Если у есть точка лок. миним. зад. (1),то матрица  , составленная их вторых частных производ. ф-ии f в точке y, неотриц. Определена,т.е. для всех
, составленная их вторых частных производ. ф-ии f в точке y, неотриц. Определена,т.е. для всех  вып. нер-во
вып. нер-во  Д-во Рассм. Приращение цел. ф-ии в т. y соотв-щее приращ. аргум.
Д-во Рассм. Приращение цел. ф-ии в т. y соотв-щее приращ. аргум.  где
где  малое,
малое,  - произв. в-ор
- произв. в-ор  Т.к. ф-я f дважды диф., тосправедливо
Т.к. ф-я f дважды диф., тосправедливо 
Т4 (достат.усл.оптим-ти). Пусть в з.(1) ф-я f(x) дважды диф-ма. Т-ка 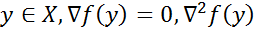 строго полож.опред-на,т.е.
строго полож.опред-на,т.е.  .Тогда y есть решение з.(1) Док-во. Пусть в т. у вып-ны усл-я т-мы, но т. y не явл. Реш. з.Это означает, что сущ. Посл-ть точек
.Тогда y есть решение з.(1) Док-во. Пусть в т. у вып-ны усл-я т-мы, но т. y не явл. Реш. з.Это означает, что сущ. Посл-ть точек  Представим
Представим  ,
,  . Рассм.
. Рассм. 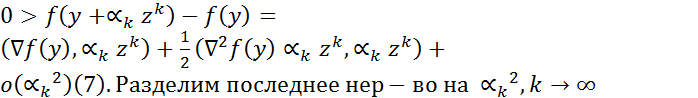 и учтем
и учтем  Получим
Получим  Получим противоречие, кот. док-ет т-му. Пример. Исслед. на экстр. ф-ю
Получим противоречие, кот. док-ет т-му. Пример. Исслед. на экстр. ф-ю  .
.  Строим матрицу 2-х произв.
Строим матрицу 2-х произв.  Подст.
Подст. 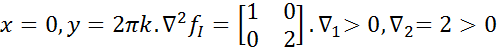 по крит.Сильвестра полож.опред. Т.
по крит.Сильвестра полож.опред. Т.  т-ки минимума.
т-ки минимума.
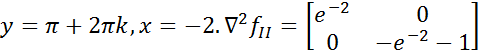 .
.  .Квадр.ф-я не явл. знакоопред. поэтому не вып-но необход.усл.2-го порядка и в т-х
.Квадр.ф-я не явл. знакоопред. поэтому не вып-но необход.усл.2-го порядка и в т-х 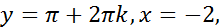 нет экстр.В т-ме3 и т-ме4 при исслед.з. на max знакоопред-ть квадр-й формы следует поменять на противоположную.
нет экстр.В т-ме3 и т-ме4 при исслед.з. на max знакоопред-ть квадр-й формы следует поменять на противоположную.
Поиск по сайту: