АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод золотого сечения решения задачи одномерной минимизации

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I Психологические принципы, задачи и функции социальной работы
  4. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  5. I. 1.1. Пример разработки модели задачи технического контроля
  6. I. 1.2. Общая постановка задачи линейного программирования
  7. I. 2.1. Графический метод решения задачи ЛП
  8. I. 3.2. Двойственный симплекс-метод.
  9. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  10. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  11. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  12. I. Метод рассмотрения остатков от деления.

МЗС позволяет решить задачу с требуемой точностью при меньшем кол-ве вычислений значения функции.

Опр. Золотым сечением отрезка наз деление отрезка на 2 неравные части так, что отношение длины меньшей части к длине большей равно отношению длины большей части к длине всего отрезка.

Т-ки, кот. делят отрезок в золотом отношении

Описание МЗС. Решаем задачу . Положим а1=а, b1=b и найдем точки х1 и х2, котор делят [a1;b1] в золотом сечении. Вычислим 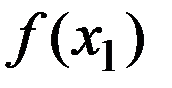и 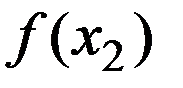. Если , то положим а2=а1, b2=x2, . Если , то а2=х1, b2=b1, . Длина построенного отрезка [a2;b2] равна 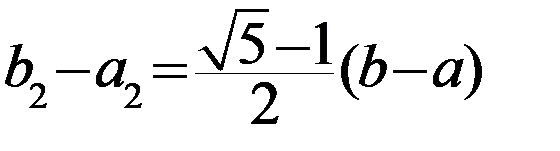и точка , кот. делит отрезок [a2;b2] в золотом отношении.

Пусть на некотор. этапе найден отр-к , найдены т-ки х1, ,…, и вычислены значения 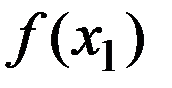, f(),…,f(). Длина отрезка . И на отрезке есть т-ка , кот. делит этот отрезок в ЗО и в кот. вычислено значение целевой функции.

Определим следующ. т-ку по правилу .

Предположим, что (). Вычислим знач. ф-ции в т-ке .Если выполняется неравенство , полагаем . Если , то , в результате получим отрезок , имеющий непустое пересечение с мн-вом решений задачи, длина кот.

Если количество вычислений значений целевой ф-ции ничем не огранич., то процесс вычислений продолжается до тех пор, пока не будет выполнятся неравенство

Если количество вычислений значений целевой ф-ции ничем огранич., то процесс вычислений заканчивается, когда будет выполнено заданное число итераций. В качестве точки минимума выбираем т-ку с вычисленным в ней значением целевой ф-ции.

Погрешность этого метода:

Замечание. Преимуществом МЗС явл. тот факт, что на каждой итерации знач. ф-ции вычисляется только один раз.

Замечание. МЗС можно применять для нахождения минимума функции не являющейся унимодальной. Но в этом случае решение может находиться далеко от глобального минимума.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)