АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Понятие решения задачи мат. программиров

Читайте также:
  1. Apгументация как логико-коммуникативный процесс. Понятие научной аргументации.
  2. FAST (Методика быстрого анализа решения)
  3. I Понятие об информационных системах
  4. I Психологические принципы, задачи и функции социальной работы
  5. I. 1.1. Пример разработки модели задачи технического контроля
  6. I. 1.2. Общая постановка задачи линейного программирования
  7. I. 2.1. Графический метод решения задачи ЛП
  8. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  9. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  10. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  11. I. ПОНЯТИЕ ДОКУМЕНТА. ВИДЫ ДОКУМЕНТОВ.
  12. I. Понятие и значение охраны труда

Пусть на некотором мн-ве 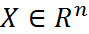задана скалярная ф-я f(x), точки 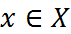назыв допустимыми, а X – допустимым, f(x) – целевая ф-я.

Задача мат-го программирования (ЗМП) заключ в нахождении min ф-ии f(x), если 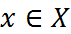. (1)

Под реш ЗМП понимают:

1) найти точку min ф-ии f(x) на мн-ве X, т.е. найт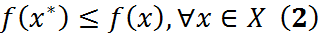и : или (3) или 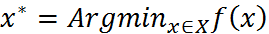(4)

2) найти точную нижнюю грань ф-и (5)

Пусть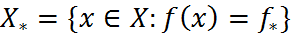

Если 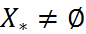, то найдя одно из значений (2) – (4), то автоматчески решается зад (5)

Если 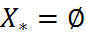, то (5) приобретает самостоятельное решение

3) Убедиться в том, что ф-я f(x) неограниченна снизу на X, т.е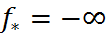

4) убедиться в том что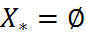

В случаях 3) – 4) говорят что задача (1) не имеет решений


 


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)