АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача вариационного исчисления с движущимся по кривой концом

Читайте также:
  1. I. 3.1. Двойственная задача линейного программирования
  2. II. Смещение кривой совокупного предложения.
  3. II.2. Задача о назначениях
  4. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  5. III Возрастание совокупного спроса на классическом отрезке кривой совокупного предложения.
  6. VI. Общая задача чистого разума
  7. Алгебраический анализ кривой IS.
  8. Анализ отрезков кривой совокупного предложения.
  9. Аналитическое выравнивание по показательной кривой
  10. Балла). Какое из утверждений о кривой совокупного спроса является НЕверным?
  11. Бюджетные ограничения кривой безразличия.
  12. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака

Рассм. задачу где 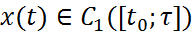,значение 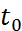задано, левый конец траектории зафиксирован , правый конец траектории явл. подвижным, то есть лежит на заданной кривой

Таким обр, необходимо найти точку и функцию , определяется на отрезке , для которых функционал достигает минимальное значение при условиях

Теор: Если 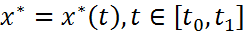явл. слабой минималью в простейшей задаче вариационного исчисления с фиксированным левым и подвижным правым концом то она уд. ур-нию Эйлера, граничным усл. и условию трансверсальности на правом конце .

Замечание Если левый конец траектории тоже является подвижным(лежит на гладкой кривой (x= 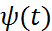), то экстремаль удовлетворяет дифференциальному уравнению Эйлера, краевым условием и условиям трансерсальности ,


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

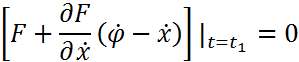
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)