АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

В этом случае уравнение Эйлера принимает вид

Читайте также:
  1. A. ЕСЛИ ВЫ ПРИНИМАЕТЕ ГОСТЕЙ У СЕБЯ ДОМА (В ХРАМЕ)
  2. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  3. IV. УРАВНЕНИЕ ГАМЛЕТА
  4. V. Требования к проведению санитарно-противоэпидемических (профилактических) мероприятий в случае выявления больного чумой на территории Российской Федерации
  5. V2: Волны. Уравнение волны
  6. V2: Уравнение Шредингера
  7. XII. Мероприятия в случае завоза дикого полиовируса, выявлении циркуляции вакцинородственных полиовирусов
  8. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  9. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  10. Анализ индивидуальных случаев
  11. Анализ случаев нарушения безопасности движения с установлением виновных и конкретных нарушений правил и порядка работы
  12. Анализ частных случаев.

.

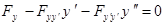Умножив обе части этого уравнения на 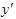, в левой части получим точную производную, то есть 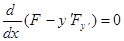, откуда

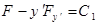, (10)

где - производная постоянная. Это уравнение может быть проинтегрировано путём разрешения относительно и разделения переменных или путем введения параметра.

Контрольные вопросы:

1. Чем отличается основная задача вариационного исчисления от конечномерной задачи?

2. Дайте графическое истолкование основной задачи вариационного исчисления.

3. Может ли вариационная задача иметь бесчисленное множество решений?

4. В каких случаях вариационная задача не имеет решений?

5. Является ли экстремаль решением основной задачи вариационного исчисления?

6. В каких случаях экстремальные кривые вырождаются в прямые?

 



1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)