Анализ частных случаев

В качестве частных случаев рассмотрим процессы чистого размножения и процессы чистой гибели.

Процесс чистого размножения с интенсивностями перехода, не зависящими от состояния, l_k=l, m_k=0, подробно исследован в Главе III. «Пуассоновский процесс (простейший поток)». Здесь заметим только, что для процесса чистого размножения множество состояний вложенной цепи Маркова образует класс несущественных состояний и поэтому интерес представляют вероятностные характеристики на конечном интервале времени.

Для процесса чистой гибели x(t) зафиксируем n>0 и положим P(x(0)=n)=1 и m_k=km, 0£k£n, l_k=0. Это значит, что рассматривается случай, когда интенсивности перехода зависят от состояния, когда процесс x(t) стартует из состояния n>0, а состояние 0 является поглощающим.

Вычислим переходные вероятности этого однородного марковского процесса Очевидно, что эти переходные вероятности отличны от нуля только для s£k. Используя уравнения Колмогорова для переходных вероятностей (4.12), при 0£s£k£n докажем равенство

(4.42)

Доказательство проведем методом математической индукции. При s=k имеем из (4.12) уравнение

единственным решением которого при начальном условии p_kk(0)=1 является функция p_kk(t)=e^-mkt, то есть при s=k равенство (4.42) справедливо. Далее предположим, что равенство (4.42) справедливо при s<k, и докажем его справедливость при s-1. Из (4.12) получаем линейное неоднородное дифференциальное уравнение

(4.43)

при начальном условии Единственным решением этого уравнения является функция

, (4.44)

что доказывается непосредственной подстановкой функции (4.44) в уравнение (4.43). Таким образом, доказано сформулированное утверждение (4.42).

Если учесть условие P(x(0)=n)=1, то получим равенство для вероятностей состояний процесса чистой гибели при 0£k£n

(4.45)

Равенству (4.45) можно дать интересную интерпретацию. Предположим, что в момент t=0 начинаются n операций, длительности которых есть независимые случайные величины, распределенные по экспоненциальному закону с параметром m. Тогда равенство (4.45) определяет вероятность того, что к моменту t ровно n-k операций закончатся, а k операций продолжаются.

В приложениях часто возникает необходимость вычислять математическое ожидание интегралов от траекторий случайного процесса.

Для процесса чистой гибели x(x) с интенсивностями переходов m_k=km, 0£k£n обозначим траектории x(x,ω) при (0,t). Обозначим через x_k,t случайное время, которое процесс x(x) провел в состоянии k. Очевидно, из определения индикатора следует, что индикатор I(ξ(x,ω)=k), 0≤x<t, есть случайная функция, равная единице в тех точках x, для которых ξ(x,ω)=k, и равная нулю в тех точках x, для которых ξ(x,ω) ≠ k. Следовательно, .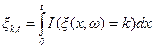

Тогда в соответствии с определением математического ожидания индикатора (математическое приложение 6) и равенством (4.45) имеем

(4.46)

При выводе последнего равенства мы воспользовались соотношением [13]

Естественно, что при t®¥ имеем равенство

Теперь легко посчитать математическое ожидание интеграла от случайного процесса чистой гибели x(x).

Прежде всего, заметим, что траектории процесса чистой гибели суть ступенчатые невозрастающие функции. Следовательно, если использовать ранее принятое обозначение - время, проведенное процессом гибели в состоянии k, k>0 на временном интервале (0,t), то по определению интеграла получаем равенство

(4.47)

При вычислении математического ожидания интеграла (4.47) используем соотношение (4.46) и получим

(4.48)

Далее исследуем условные математические ожидания времени пребывания процесса x(x) в фиксированном состоянии и интеграла от этого процесса при условии, что реализовалось событие k£n.

При k£s£n и 0£x£t имеем

(4.49)

так как

При выводе формулы (4.49) мы использовали интерпретацию равенства (4.44): к моменту x должны закончиться ровно n-s операций, и за оставшееся время t-x должно закончиться еще ровно s-k (из оставшихся s операций), при этом используется замечательное свойство экспоненциального распределения - оставшаяся длительность s операций, не закончившихся к моменту x,имеет экспоненциальное распределения с тем же параметром m.

Имея условные вероятности (4.49), интегрированием вычисляем математическое ожидание времени пребывания процесса в состоянии s, k≤s≤n при условии, что реализовалось событие

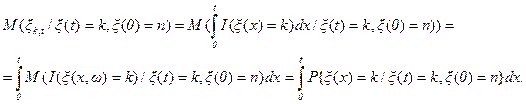(4.50)

При вычислении условного математического ожидания интеграла от траектории случайного процесса используем равенство (4.47)

(4.51)

что с учетом равенств (4.49) и (4.50) позволяет выразить искомые условные математические ожидания через исходные параметры.

Поиск по сайту: