Исследование условных и безусловных математических ожиданий

Исследуем математические ожидания при условии, что на интервале (0,t) произошло ровно n восстановлений, то есть реализовалось событие

Из условного распределения (3.25) случайной величины получаем условное математическое ожидание для 0<k£n

(3.28)

где обозначена через B_k,n(1) полная бета-функция и использована связь гамма и бета-функций для целых параметров k и n

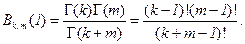
По определению , потому из (3.28) следует

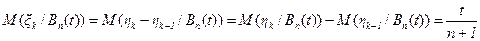, (3.29)

то есть получили, что условное математическое ожидание интервалов между соседними моментами восстановления для простейшего потока не зависит от номера этого интервала.

Аналогичный результат получим, если воспользуемся для вычисления условного математического ожидания M(x_k/B_n(t)), k£n, равенством 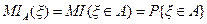для математического ожидания индикатора некоторого события (математическое приложение 6)

Рассмотрим траектории простейшего потока x(x,ω), для которых на интервале (0,t) произошло ровно n событий (реализовалось событие B_n(t)). Очевидно, из определения индикатора следует, что индикатор I(ξ(x,ω)=k-1), 0≤x<t, есть случайная функция, равная единице в тех точках x, для которых ξ(x,ω)=k-1, и равная нулю в тех точках x, для которых ξ(x,ω) ≠ k-1. Следовательно, 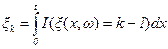. Тогда имеем

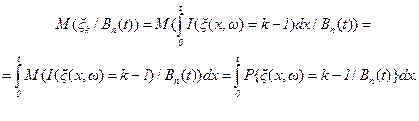(3.30)

В выше приведенной цепочке равенств перестановка порядка интегрирования законна в силу абсолютной сходимости интегралов.

Далее вычислим условную вероятность . Из (3.1) и независимости приращений простейшего потока получаем

(3.31)

Интегрируя функцию (3.31), получаем соотношение (3.29).

Представляет интерес и безусловное математическое ожидание времени, проведенного процессом x(x) в состоянии k, k³0 на периоде (0,t). Обозначим через время, проведенное Пуассоновским процессом в состоянии k-1, k>0 на временном интервале (0,t). Из равенства получаем

(3.32)

Равенство (3.32) позволяет получить очевидное тождество

так как числитель есть функция восстановления Пуассоновского процесса.

Исследуем математические ожидания при условии, что на интервале (0,t) произошло по крайней мере n восстановлений, то есть реализовалось событие

Вычислим условное математическое ожидание 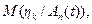0<k£n. Для решения этой задачи можно воспользоваться равенством (3.27), так как

.

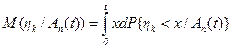С другой стороны, учитывая связь между событиям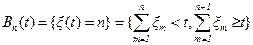и и можно непосредственно перейти к вычислению математического ожидания. Тогда получим

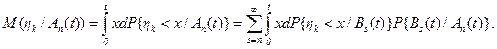
Равенство (3.28) определяет условное математическое ожидание

а условная вероятность для простейшего потока при s<n равна

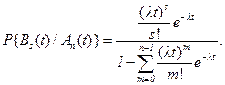
Таким образом, для искомого условного математического ожидания получаем равенство для

(3.33)

Из равенства (3.33) следует для

(3.34)

то есть получили, что условное математическое ожидание интервалов между соседними моментами восстановления для простейшего потока также не зависит от номера этого интервала.

В заключение раздела приведем выражения для математических ожиданий (безусловного и условного) интегралов от пуассоновского процесса в конечных пределах.

Прежде всего заметим, что траектории простейшего потока суть ступенчатые неубывающие функции. Следовательно, если использовать ранее принятое обозначение - время, проведенное Пуассоновским процессом в состоянии k-1, k>0 на временном интервале (0,t), то по определению интеграла получаем равенство

(3.35)

При вычислении математического ожидания интеграла (3.35) используем соотношение (3.32) и получим

(3.36)

При вычислении условного математического ожидания интеграла (3.35) при условии, что на интервале (0,t) произошло ровно n восстановлений, используем соотношение (3.29) и получим

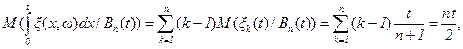(3.37)

поскольку при k>n.

Поиск по сайту: