Узловая теорема восстановления

При решении ряда практических и теоретических задач возникает необходимость перехода к пределу в интеграле свертки тогда, когда подынтегральные функции не являются ограниченными функциями на бесконечности. В частности, в теории восстановления возникают интегралы вида

. (2.28)

Если процесс восстановления не является обрывающимся, т.е. распределение F(x) собственное, F(¥)=1, и существует математическое ожидание Mx,, то функция восстановления H(t) не ограничена на бесконечности, и в соответствии с элементарной теоремой восстановления в бесконечности она растет как линейная функция. В этом случае непосредственно воспользоваться леммой 2.2, приведенной в предыдущем разделе, нельзя. В настоящем разделе приведем без доказательства две теоремы - теорему Блекуэлла и узловую теорему восстановления, ликвидирующие этот пробел. Доказательства можно найти в [6].

Прежде чем переходить к формулировке теорем дадим определение арифметического распределения.

ОПРЕДЕЛЕНИЕ 2.1. Дискретное распределение случайной величины x, определяемое последовательностью значений и вероятностями , k>0, называется арифметическим (решетчатым), если существует такое С и такое h>0, что для любого x_n справедливо представление x_n=C+k_nh, где k_n целое число.

Распределения, не обладающие этими свойствами, неявляются арифметическими. В частности, непрерывное распределение не является арифметическим. В дальнейшем такие распределения будем называть нерешетчатыми.

Смысл арифметического (решетчатого) распределения заключается в том, что для такого распределения можно выбрать новое начало координат (выбор константы С) и новый масштаб (выбор константы h), при которых значения, принимаемые случайной величиной, будут целыми.

ТЕОРЕМА БЛЕКУЭЛЛА. Если распределение F(t)=P{x<t} является нерешетчатым, то при любом фиксированном h>0

. (2.29)

УЗЛОВАЯ ТЕОРЕМА ВОССТАНОВЛЕНИЯ. Пусть Q(x) неотрицательная невозрастающая интегрируемая функция, существует интеграл и распределение F(t)=P{x<t} нерешетчатое, тогда

. (2.30)

Здесь же докажем эквивалентность сформулированных теорем.

Если положить , то очевидно из (2.30) следует (2.29).

Далее предположим, что справедливо предельное соотношение (2.29). Тогда разность H(t+h)-H(t)<N(h)<¥ равномерно ограничена при любых h>0. По условию теоремы lim_t®¥Q(t)=0.

При фиксированных h>0 и k³0 определим функцию q_k(t,h)=1 при kh£x<(k+1)h и q_k(t,h)=0 вне этого интервала. В этих обозначениях в силу монотонности подынтегральной функции получаем двустороннюю оценку

Тогда для интеграла имеем следующие оценки

(2.31)

где через обозначена целая часть отношения.

При фиксированных h>0 и n³0, если t велико, t>t(n), из (2.31) получаем

(2.32)

Перейдем в (2.32) к пределу при t®¥ и получим в силу справедливости (2.29)

(2.33)

В силу интегрируемости функции Q(x) имеем

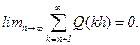(2.34)

Поэтому при переходе в (2.33) к пределу при n→∞ получаем

что при при h→0 доказывает предельное равенство (2.30).*

Поиск по сайту: