Определение марковского процесса

Марковский случайный процесс, как и произвольный случайный процесс, должен задаваться семейством согласованных конечномерных распределений. Однако, в силу того, что он обладает специфическим марковским свойством, его можно задать частными характеристиками - переходными вероятностями.

Переходим к формальному определению.

ОПРЕДЕЛЕНИЕ 4.1. Случайный процесс x(t) с непрерывным временем и дискретным множеством состояний Е (конечным или счетным) называется марковским, если для любого целого n>0, любого набора моментов и любого набора состояний для условных вероятностей справедливо равенство

. (4.1)

Марковское свойство (4.1) позволяет доказать при k>0 равенство (4.2)

В самом деле, с учетом (4.1) получаем из определения условной вероятности

Таким образом, равенство (4.2) доказано. При k=1 равенства (4.1) и (4.2) совпадают.

Из равенства (4.2) по определению условной вероятности легко получаем при 0<n<k соотношение

(4.3)

Докажем обратное, что из равенства (4.3) следует равенства (4.2) и (4.1). Из определения условной вероятности получаем при выполнении (4.3).

Первое равенство выполняется в силу предположения справедливости (4.3), последующие равенства следуют из определения условной вероятности.

Таким образом, получаем равенство

утверждающее, что из соотношения (4.3) следует (4.2).

Получили доказательство эквивалентности равенств (4.1) и (4.3). Другими словами, марковское свойство можно определять как равенство (4.3).

Если считать момент t_n - настоящим моментом, состояние e_n - настоящее значение процесса, то равенство (4.3) можно интерпретировать как независимость прошлого и будущего течения процесса при известном настоящем. Это свойство часто считают определением марковского свойства случайного процесса. Точный математический смысл его выражает равенство (4.3).

Замечание 1. Отметим, что все введенные выше условные вероятности и полученные равенства предполагали, вероятности условий не равны нулю.

Замечание 2. При исследовании процессов Маркова вводится понятие строго марковского свойства. Если при введении марковского свойства процесса (см. равенство (4.3)) настоящее определялось произвольным неслучайным моментом t и значением процесса в этот момент времени , то для выполнения строго марковского свойства настоящее определяется значением процесса в случайный момент времени.

Не ограничивая общности, в дальнейшем множество состояний Е будем считать множеством положительных целых чисел.

В правой части равенства (4.1) стоит функция P{x(t)=j½x(x)=i}, t>x, которая называется переходной вероятностью. Эта функция в общем случае зависит от параметров x,tÎ[0,¥), и i,jÎE. Обозначим переходную вероятность через

ОПРЕДЕЛЕНИЕ 4.2. Марковский процесс называется однородным, если переходная вероятность зависит от разности аргументов t и x

(4.4)

Из определения переходных вероятностей вытекают их свойства при 0<t<¥

·

·

При конечном множестве состояний Е последнее свойство тривиально, при бесконечном множестве состояний Е последнее свойство означает, что за конечное время процесс с вероятностью единица перейдет в некоторое конечное состояние.

В дальнейшем будем также предполагать непрерывность вероятностей при t>0 и равенства

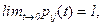если i=j, если i¹j. (4.5)

Из марковского свойства и определения переходных вероятностей следует, что для однородных марковских процессов имеет место равенство при t>0 и x>0

(4.6)

Свойство (4.6) называют уравнениями Колмогорова-Чепмена.

Если задать распределение вероятностей состояний марковского процесса в начальный (нулевой) момент времени

(4.7)

то для одномерного распределения по формуле полной вероятности получаем

Покажем, что задание начального распределения (4.7) и семейства матриц переходных вероятностей

(4.8)

позволяет построить согласованные конечномерные распределения марковского однородного случайного процесса x(t).

По формуле полной вероятности для любого n>0 и любых наборов 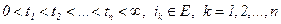с учетом марковского свойства и однородности получаем

(4.9)

Равенство (4.9) доказывает высказанное утверждение и, следовательно, однородный марковский процесс задается начальным распределением (4.7) и семейством матриц переходных вероятностей (4.8).

Поиск по сайту: