АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Прямое время возвращения (перескок)

Читайте также:
  1. B15 (высокий уровень, время – 10 мин)
  2. Can (прош. время could)
  3. Can (прош. время could)
  4. I. МЕСТО И ВРЕМЯ КАК ГРАНИЧНЫЕ УСЛОВИЯ
  5. I. Опровержение тезиса (прямое и косвенное)
  6. III. Новое время
  7. III. Требования охраны труда во время работы
  8. IV. Аппетит, извращения вкуса, насыщение во время приема пищи
  9. May (прош. время might)
  10. T (время)
  11. XVI-XVII вв. в мировой истории. «Новое время» в Европе
  12. А безумие систематично, во время сна все связано.

Прямое время возвращения xt (время передоскока) определяется как время от момента t до ближайшего восстановления, произошедшего после t. Заметим, что при любом x>0 событие {xt>x} означает, что на интервале (t,t+x) нет восстановлений. Искомое распределение выпишем, используя формулу полной вероятности. Для условных вероятностей имеем при x³0, 0£y£t

,

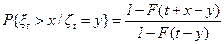при этом учитывается, что на периоде [y,t) нет восстановлений.

Тогда по формуле полной вероятностей получаем

или для функции распределения получаем

(2.41)

Из (2.41) получаем выражение для математического ожидания

(2.42)

Здесь уместно привести выражение для математического ожидания интервала, накрывающего точку t. Из равенств (2.40) и (2.42) получаем сумму

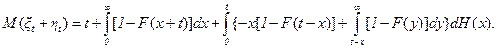(2.43)

Отметим одно важное обстоятельство - математическое ожидание этого интервала не совпадает с математическим ожиданием случайной величины x.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)