Стационарные процессы восстановления

ОПРЕДЕЛЕНИЕ 2.2. Стационарным процессом восстановления x(t) называется такой процесс восстановления, у которого распределение числа восстановлений, произошедших на любом интервале заданной длины, не зависит от расположения этого интервала, т.е. функция P{x(t+x)-x(t)=k} не зависит от t, а зависит только от x и k.

В теории случайных процессов такие процессы называют процессами со стационарными приращениями или однородными процессами [8]. В теории массового обслуживания, следуя Хинчину [5], такие потоки называют стационарными. Мы будем придерживаться этой терминологии, поскольку ориентируемся на литературу по теории массового обслуживания.

Обозначим через H₁(t) функцию восстановления стационарного процесса восстановления ξ(t). При H₁(0)=0 получаем

M[x(t+x)-x(t)]=H₁(t+x)-H₁(t)=H₁(x)=M[x(x)-x(0)].

Первое равенство следует из определения функции восстановления процесса восстановления, а второе равенство следует из определения стационарности процесса восстановления.

Поэтому для функции восстановления стационарного процесса восстановления справедливо равенство H₁(t+x)=H₁(t)+H₁(x). Единственной функцией, тождественно не равной константе и удовлетворяющей этому соотношению, является линейная функция , поскольку коэффициент определяется поведением функции восстановления в бесконечности (см. элементарную теорему восстановления). Определим, какие функции (F₁(x), F(x)) задают процесс восстановления с запаздыванием, у которого функция восстановления линейная функция. Для этого подставим функцию в интегральное уравнение восстановления (2.17) и получим распределение F₁(x), соответствующее заданной функции восстановления,

или

. (2.59)

Итак, получили соотношение (2.59), устанавливающее связь между функциями F₁(x) и F(x), если процесс восстановления стационарный. Другими словами, задавая функцию F(x), получаем функцию распределения первого интервала F₁(x) для стационарного процесса восстановления. Условие (2.59) является необходимым условием стационарности процесса восстановления, то есть, если процесс восстановления стационарен, то справедливо равенство (2.59).

Равенство (2.59) позволяет утверждать, что для стационарного процесса восстановления функция F₁(x) должна быть дифференцируемой и, следовательно, справедливо равенство

.

Следовательно, обратно, задавая F₁(x) и константу ,получаем функцию F(x), длякоторой процесс восстановления будет стационарным.

Докажем, что (2.59) является и достаточным условием стационарности процесса восстановления.

Итак, предположим, что задан процесс восстановления с запаздыванием, у которого функции распределения, его определяющие, F₁(x) и F(x) связаны соотношением (2.59). Тогда получаем связь между преобразованиями Лапласа-Стилтьеса

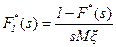
и из (2.20) получаем преобразование Лапласа-Стилтьеса функции восстановления стационарного процесса восстановления

(2.60)

Единственной функцией, у которой преобразование Лапласа-Стилтьеса (2.54) и H₁(0)=0, является линейная функция .

Далее заметим, что равенства (2.36), (2.39) и (2.41), выведенные выше для простого процесса восстановления, легко переносятся на процесс восстановления с запаздыванием. Приведем их без подробного объяснения

, при 0<x£ t, (2.61)

при 0<x£ t,(2.62)

при x>0. (2.63)

Если в равенство (2.63) подставить функцию (2.59) и линейную функцию восстановления , то получаем . Это значит, что развитие процесса восстановления на интервалах (0,x) и (t,t+x) определяется одними и теми же вероятностными характеристиками. Тогда совпадут распределения числа восстановлений, произошедших на этих интервалах. Следовательно, процесс восстановления стационарный. Таким образом, доказана следующая

ТЕОРЕМА 2.3. Процесс восстановления стационарен тогда и только тогда, когда функции F₁(x) и F(x), определяющие его, связаны соотношением (2.59).

Сформулированные выше необходимые и достаточные условия стационарности процесса восстановления могут быть взяты за определение его стационарности.

Поиск по сайту: