Примеры полумарковских процессов

1. Процесс восстановления (принятые определения и обозначения приведены в главе II). Для простого процесса восстановления N(t), определяемого как число восстановлений, произошедших до момента t, полумарковское ядро имеет вид

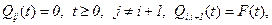
где F(t) – функция распределения положительных независимых одинаково распределенных случайных величин x₁,x₂,…,x_k,…, образующих процесс восстановления.

Если использовать введенные выше обозначения, то получим

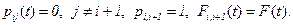
Для процесса восстановления N₁(t) с запаздыванием, определяемого как число восстановлений, произошедших до момента t, полумарковское ядро имеет вид

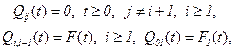
где 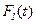– функция распределения случайной величины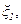 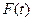– функция распределения положительных независимых случайных величин 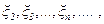образующих процесс восстановления с запаздыванием.

2. Марковская цепь. Однородная цепь Маркова с матрицей переходных вероятностей есть полумарковский процесс с полумарковским ядром

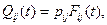
где

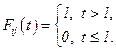
3. Марковский процесс с непрерывным временем и дискретным множеством состояний (принятые определения и обозначения приведены в главе IV).

Для марковского процесса с интенсивностями перехода 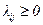при i№j, l_ii=0 в соответствии с равенством (4.22) имеем

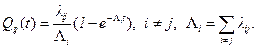
Поиск по сайту: