 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Совместное распределение прямого и обратного времен возвращения
Для 0£x£t, y³0 выпишем вероятности P{xt³y,ht³x}, из которых легко получить совместное распределение P{xt<y,ht<x}. В самом деле,
P{xt³y,ht³x}+P{xt<y,ht<x}+P{xt³y,ht<x}+P{xt<y,ht³x}=1
P{xt<y}=P{xt<y,ht<x}+P{xt<y,ht³x},
P{ht<x}=P{xt<y,ht<x}+P{xt³y,ht<x}.
P{xt³y,ht³x}+P{xt<y}+P{ht<x}-1=Pxt<y,ht<x}.
Для того, чтобы реализовалось событие {xt³y}Ç{(ht³x}, необходимо и достаточно отсутствия восстановлений на интервале (t-x,t+y). Поэтому,
(2.44)
Так как случайная величина ht имеет положительный атом при x=t, то особо надо выделить случай
P{xt³y,ht=t}=1-F(t+y),
что соответствует первому слагаемому в (2.44).
Наконец, при x>t, y³0 совместная вероятность 
равна нулю в силу равенства (2.42).
Равенство (2.44) показывает зависимость случайных величин xt и ht, так как вероятность не представима в виде произведения вероятностей 
и 
.
В заключение настоящего раздела приведем распределение интервала, накрывающего произвольный момент t, то есть распределение суммы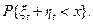 
При x<t получаем
(2.45)
При 
получаем
(2.46)
Поиск по сайту: