Определение и свойства простейшего потока

ОПРЕДЕЛЕНИЕ 3.1. Простейшим потоком x(t) называется простой процесс восстановления, у которого интервалы между моментами восстановления распределены по экспоненциальному закону F(x)=1-e^-lt, t³ 0 с параметром l.

Из определения следует, что простейший поток определяется своим параметром и один простейший поток отличается от другого значением этого параметра.

Переходим к изучению свойств этого процесса.

1. Стационарность. Для доказательства стационарности нужно проверить выполнение необходимого и достаточного условия (2.59). Выполнение условия (2.59) очевидно, то есть F₁(x)=1-e^-lt, t³0.

Далее докажем, что простейший поток является единственным простым процессом восстановления, обладающим свойством стационарности.

Для любой функции распределения F(x) обозначим 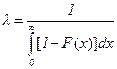и из (2.59) для простого процесса восстановления с распределением F(x) дифференцированием получим дифференциальное уравнение

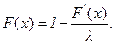
Для этого дифференциального уравнения единственным решением с начальным условием F(0)=0 является функция F(x)=1-e^-lx, x³0. Это и доказывает наше утверждение.

Используя свойство стационарности, можно изучать этот процесс восстановления на интервале (0,t), поскольку P{x(t)=k}=P{x(t+x)-x(x)=k}. Так как P{x(t)=k}=P{h_k<t,h_k+1³t}, 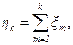x_m - последовательность независимых случайных величин, распределенных по экспоненциальному закону с параметром l, то в силу равенства (1.10) получаем

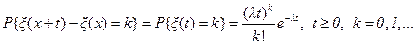, (3.1)

то есть число восстановлений на произвольно расположенном интервале (x,x+t) распределено по закону Пуассона с параметром lt.

Функция восстановления простейшего потока равна

H(t)=lt, (3.2)

что следует непосредственно из (3.1) и определения функции восстановления (2.2)

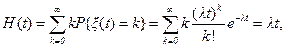
либо как решение уравнения восстановления (2.16), из которого получаем преобразование Лапласа-Стилтьеса 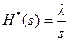, так как 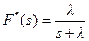, и, следовательно, равенство (3.2).

2. Отсутствие последействия. Это свойство характеризует независимость прошлого и будущего течения процесса восстановления. Для процессов восстановления это свойство можно назвать марковским свойством.

Зафиксируем момент t>0 и все поведение процесса до момента t будем называть прошлым, а после момента t - будущим.

Выпишем функцию распределения момента z последнего восстановленияна интервале [0,t). С учетом (3.2) из равенств (2.35) и (2.36) для простейшего потока имеем

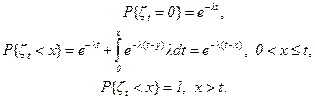(3.3)

С учетом (3.3) или (2.37) имеем для математического ожидания момента последнего восстановления

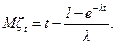
Для обратного времени возвращения h_t (времени недоскока) имеем из (2.38) и (2.39)

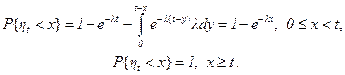(3.4)

Из последнего соотношения следует равенство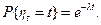

С учетом (3.4) или (2.40) имеем для математического ожидания времени недоскока

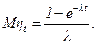
При t®¥ распределение времени недоскока простейшего потока стремится к экспоненциальному распределению с параметром l, а математическое ожидание стремится к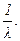

Заметим, что случайные величины z_t и h_t определяют поведение процесса восстановления в прошлом.

Далее вычислим распределение времени перескока x_t - случайной величины, определяющей поведение процесса восстановления в будущем. Из (2.41) и (2.42) получаем

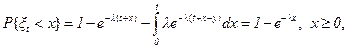(3.5)

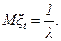
Теперь исследуем зависимость прошлого и будущего поведения простейшего процесса. Для этого вычислим совместное распределение x_t и h_t, воспользовавшись равенствами (2.44). Получаем при 0<x£t, y>0

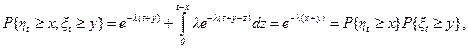(3.6)

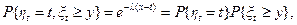(3.7)

наконец, 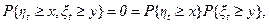при x>t, y>0.

Последние равенства доказывают независимость случайных величин x_t и h_t для простейшего потока и свойство отсутствия последействия для этого потока.

Это свойство можно переформулировать как свойство независимости приращений простейшего потока x(t) на произвольных непересекающихся интервалах времени (0,x) и (x,x+t), x³0, t³0, n³0, k³0

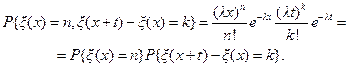(3.8)

3. Ординарность. Как и всякий процесс восстановления, простейший поток имеет неубывающие ступенчатые траектории (напомним, что x(t) есть число восстановлений, произошедших до момента t) и, коль скоро экспоненциальное распределение непрерывно в нуле, то вероятность того, что интервал между соседними моментами восстановления равен нулю, равна нулю. Значит, почти все траектории простейшего процесса будут иметь скачки, равные единице. Свойство ординарности определяется как свойство, выражаемое асимптотическим равенством P{x(t)>1}=o(t) при t®0, то есть вероятность появления более одного восстановления в интервале длины x стремится к нулю быстрее, чем длина этого интервала. Из (3.1) для простейшего потока получаем

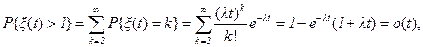(3.9)

то есть простейший поток обладает свойством ординарности.

Итак, подводя итог настоящему разделу, можно сказать, что из определения простейшего потока как процесса восстановления с экспоненциальным распределением интервалов между соседними восстановлениями, следует, что этот процесс обладает свойствами стационарности, ординарности и отсутствия последействия.

Поиск по сайту: