 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение экспоненциального распределения и его свойства
Среди распределений, при исследовании Марковских и полумарковских процессов, процессов массового и технического обслуживания, особое место занимает экспоненциальное распределение.
Случайная величина x имеет экспоненциальное распределение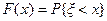 
с параметром l>0, если
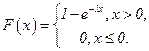. (1.1)
Экспоненциальное распределение имеет плотность
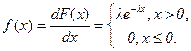(1.2)
и имеет моменты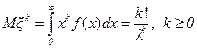 
(напомним, что по определению 0!=1). В частности, для этого распределения справедливы равенства для математического ожидания 
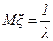, для второго момента 
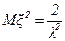, для дисперсии 
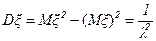и для среднеквадратического отклонения 
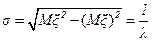, которое для рассматриваемого распределения совпадает с математическим ожиданием.
Экспоненциальное распределение обладает рядом свойств, которые присущи только ему.
Для положительной случайной величины x с произвольным распределением F(x), F(0)=0, имеющим плотность f(x), введем в рассмотрение функцию
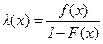,(1.3)
при тех значениях переменной x³0, для которых F(x)<1. В математической теории надежности эта функция называется интенсивностью отказов.
Учитывая следующее из определения производной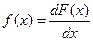 
асимптотическое равенство P{x£x<x+D}=F(x+D)-F(x)=f(x)D+o(D) при D®0, получаем асимптотическое равенство для условной вероятности P{x£x<x+D½x³x}=l(x)D+o(D) при D®0 или 
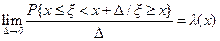. Очевидно, что для экспоненциального распределения функция l(x) не зависит от x, l(x)=l. Это следует непосредственно из определения (1.3).
С другой стороны дифференциальное уравнение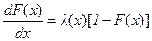 
при l(x)=l имеет единственным решением с начальным условием F(0)=0 функцию F(x)=1-e-lx при x³0. Следовательно, экспоненциальное распределение является единственным распределением, у которого интенсивность отказов постоянна (не зависит от x).
Если случайная величина x имеет экспоненциальное распределение (1.1) с параметром l>0, то при t³0, x³0 имеет место равенство
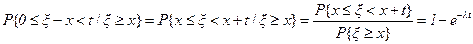,(1.4)
то есть для экспоненциально распределенной случайной величины x условное распределение случайной величины x-x (1.4)совпадает с безусловным распределением (1.1). Это свойство называется свойством отсутствия последействия. Из (1.4) следует, что для экспоненциального распределения F(x) справедливо равенство
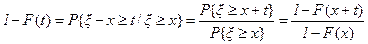
или
1-F(x+t)=[1-F(x)][1-F(t)] (1.5)
Так как равенство (1.5) выполняется только для семейства экспоненциальных функций 1-F(x)=e-lx, x³0, 0<l<¥, и констант, то можно сделать вывод о том, что экспоненциальное распределение является единственным распределением, обладающим свойством отсутствия последействия.
Поиск по сайту: