Обрывающиеся процессы восстановления

До сих пор ограничениями были:

· отсутствие у функции распределения F(t) единичного скачка в нуле для существования функции восстановления;

· существование моментов для справедливости асимптотического разложения этой функции.

При этих условиях процесс восстановления будет развиваться во времени, за конечное время произойдет конечное число восстановлений (не будет бесконечных накоплений), а за бесконечное время произойдет бесконечное число восстановлений, то есть при t®¥ с вероятностью единица x(t)®¥.

Такая ситуация имеет место, когда распределение, определяющее процесс восстановления, является собственным, то есть P{x<¥}=lim_t®¥F(t)=F(¥)=1 (условие, необходимое для существования моментов).

Другая картина возникает в случае, когда распределение F(t) является несобственным, F(¥)<1, P{x=¥}=1-F(¥)>0. Тогда с положительной вероятностью 1-F(¥)>0 процесс восстановления может оборваться на каком-то шаге, то есть время до следующего восстановления будет равно бесконечности.

Процесс восстановления, у которого распределение интервалов между соседними моментами восстановления является несобственным, называется обрывающимся процессом восстановления.

Прежде чем формулировать теорему о предельном поведении обрывающегося процесса восстановления, докажем лемму о предельном поведении интегралов свертки.

ЛЕММА 2.2. Если функции А(x) и В(x) при x>0 положительные неубывающие и равномерно ограниченные, то

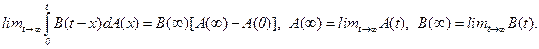
ДОКАЗАТЕЛЬСТВО. В силу условий теоремы для любого e₁>0 найдется такое t₁(e₁)>0, что при t>t₁(e₁)

.

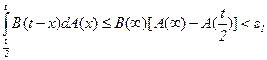Для любого e₂>0 найдется такое t₂(e₂)>0, что при t>t₂(e₂) и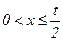

.

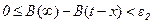Тогда при t>max[t₁(e₁), t₂(e₂)] имеем оценку

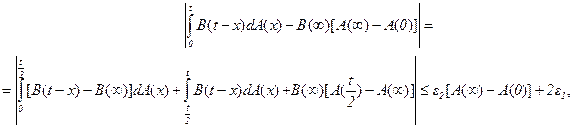
что и доказывает утверждение леммы. *

ТЕОРЕМА 2.2. Для обрывающегося процесса восстановления, начинающегося в момент t=0, справедливы следующие утверждения:

1. процесс оборвется с вероятностью единица или с вероятностью единица за бесконечное время произойдет конечное число восстановлений, то есть

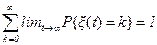; (2.24)

2. функция восстановления ограничена на расширенной полупрямой [0, ¥] и

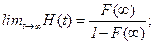(2.25)

3. момент обрыва имеет собственное распределение

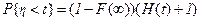. (2.26)

ДОКАЗАТЕЛЬСТВО. Для несобственного распределения непосредственный переход к пределу при t→∞ в интеграле свертки дает F^(k)(¥)=[F(¥)]^k<1, k>0, и F⁽⁰⁾(¥)<1. Доказательство этого факта легко провести по индукции, используя лемму 2.2. Функции распределения удовлетворяют условиям леммы. Поэтому 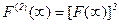. Если 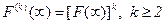, то из утверждения леммы следует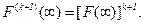

Тогда из (2.3) получаем

P{x(¥)=k}=lim_t®¥ P{x(t)=k}=lim_t®¥ [F^(k)(t)-F^(k+1)(t)]=(F(¥))^k[1-F(¥)] (2.27)

и, следовательно, справедливо (2.24).

Для доказательства (2.25) воспользуемся равенством (2.4)

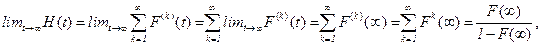
причем перемена порядка суммирования и перехода к пределу законна, поскольку ряд (2.4) сходится равномерно при 0£t<¥.

Равенство (2.27) показывает, что число слагаемых x_m до обрыва процесса восстановления имеет геометрическое распределение. Тогда по формуле полной вероятности получаем

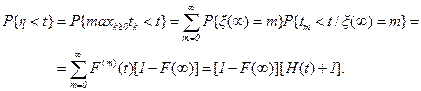
При вычислении условной вероятности , 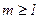заметим, что справедливо равенство событий

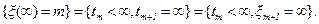
Поэтому в силу независимости случайных величин ξ_m+1 и t_m имеем

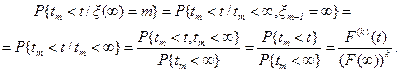
Таким образом, все утверждения теоремы доказаны. *

СЛЕДСТВИЕ 2.1. Если неубывающая функция В(x) имеет предел при x®¥, B(¥)=lim_x®¥B(x) и H(x) функция восстановления обрывающегося процесса восстановления, то

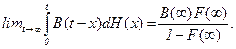
ДОКАЗАТЕЛЬСТВО. Доказательство непосредственно вытекает из равенства (2.25) и утверждения леммы 2.2.*

Поиск по сайту: