 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Альтернирующие процессы восстановления
ОПРЕДЕЛЕНИЕ 2.3. Альтернирующим процессом восстановления называется поток с ограниченным последействием, у которого
F2k-1(t)=F(t), F2k(t)=G(t), k=1,2,3,..., F(t)¹ G(t). (2.64)
Таким образом, альтернирующий процесс восстановления задается распределением F(x) нечетных интервалов и распределением G(x) четных интервалов между соседними моментами восстановления.
Нетрудно заметить, что поток четных восстановлений альтернирующего процесса образует простой процесс восстановления с распределением интервалов, равным свертке распределений F(t) и G(t),
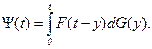(2.65)
Поток нечетных восстановлений альтернирующего процесса образует процесс восстановления с запаздыванием, определяемый функциями F(t) и Y(t).
Обозначим H0(t) и H1(t) функции восстановления этих потоков и H(t)=H0(t)+H1(t) функцию восстановления альтернирующего процесса. В силу (2.16) и (2.19)
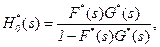
поскольку Y*(s)=F*(s)G*(s).
Из равенств (2.17) и (2.20) получаем
и, следовательно,
Если воспользоваться равенствами (2.22) и (2.53), то получим
Следовательно, для функции восстановления альтернирующего процесса восстановления будем иметь следующее асимптотическое разложение
Далее исследуем вероятность того, что произвольный момент t>0 накрывается нечетным интервалом восстановления. Для этого введем в рассмотрение следующие события
.
Тогда событие A, состоящее в том, что момент t накрывается нечетным интервалом восстановления, можно записать как сумму несовместных событий Ak, т.е. 
. Поэтому
.
Так как при k>0, то
. (2.66)
Для вероятности P2(t) противоположного события - момент t накрывается четным интервалом справедливо равенство
,
(2.67)
если провести рассуждения, аналогичные рассуждениям, проведенным при выводе (2.66), для альтернирующего процесса как процесса восстановления с запаздыванием.
Равенства (2.66) и (2.67) используем для исследования предела limt®¥Pn(t), n=1,2. Для определения предела интеграла воспользуемся узловой теоремой восстановления. Если хотя бы одно распределение F(x) или G(x) нерешетчатое и существуют их математические ожидания, то пределы существуют и
, n=1,2. (2.68)
Поиск по сайту: