Функция восстановления и ее свойства

Обозначим для простого процесса восстановления через H(t)=Mx(t) математическое ожидание числа восстановлений, произошедших до момента t, t³0. Это математическое ожидание будем далее называть функцией восстановления. Тогда по определению математического ожидания имеем

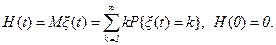(2.2)

Очевидно, все траектории процесса восстановления являются неубывающими функциями, поэтому неубывающей будет и функция восстановления,

Обозначим через B_k(t)={t_k<t}, k>0, событие, состоящее в том, что на интервале (0,t) произойдет, по крайней мере, k восстановлений. Так как по определению 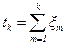и в силу того, что случайные величины x_k положительны, между событиями B_k(t)={t_k<t}, k>0 справедливы соотношения B_k(t)ÉB_k+1(t), то есть выполнение события B_k+1(t) влечет за собой выполнение события B_k(t). Тогда

причем события, стоящие в правой части этого равенства, несовместны. Следовательно, получаем

P{t_k<t,t_k+1³t}= P{t_k<t}-P{t_k+1<t}=P{x(t)=k}, (2.3)

так как событие {t_k<t,t_k+1³t} означает, что на интервале (0,t) произойдет ровно k, k³0 восстановлений, то есть {t_k<t,t_k+1³t}={x(t)=k}.

Докажем лемму о представлении и существовании функции восстановления.

ЛЕММА 2.1. Если для распределения F(t), определяющего простой процесс восстановления, существует x>0 такое, что F(x)<1, то для любого конечного t, 0<t<¥, функция восстановления конечна, H(t)<¥, и

, (2.4)

где через F^(k)(t) обозначена k-кратная свертка распределения F(t), F⁽¹⁾(t)=F(t).

ДОКАЗАТЕЛЬСТВО. По определению F^(k)(t)=P{t_k<t}. Следовательно, подставляя (2.3) в (2.2) и учитывая, что сумма ряда есть предел частных сумм, получаем

. (2.5)

Для любых t>0, x>0 найдется целое k, k>0, для которого (k-1)x<t£ kx. Имеет место следующее очевидное соотношение между событиями

, (2.6)

поскольку 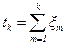и случайные величины x_j неотрицательны. Из последнего соотношения для событий в силу независимости случайных величин x_j и неравенства F(x)<1 получаем оценку для свертки

F^(k)(t)£1-[1-F(x)]^k<1, k>0. (2.7)

Заметим, что в (2.7) величины x, t и k связаны соотношением 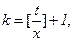где символом [a] обозначена целая часть числа a. По определению целой части справедливо неравенство [a]£a. Причем отметим, что при t>0, x>0 параметр k>0.

Далее имеем. Случайные величины x_j неотрицательны, поэтому F⁽ⁿ⁾(t)£F^(m)(t) при n>m.

Последнее неравенство вытекает из следующего утверждения (более подробно см. доказательство леммы 2.3):

если при любом t>0 имеет место неравенство для двух распределений положительных случайных величин , то , так как

.

При m>0 обозначим и целую часть отношения, k>0. Из этого определения следует неравенство , так как .

Тогда справедлива цепочка неравенств

(2.8)

При выводе (2.8) использованы следующие свойства случайных величин:

· Случайные величины x_j неотрицательны, поэтому F⁽ⁿ⁾(t)£F^(m)(t) при n>m;

^· Случайные величины z_т независимы, одинаково распределены, P{z_т<t}=F^(k)(t);

^· Для случайных величин z_т справедливы неравенства, .

Тогда из (2.8) и неравенства n£b(n,k)+1 (по определению целой части числа) получаем оценку

nF⁽ⁿ⁺¹⁾(t)£[b(n,k)+1][1-[1-F(x)]^k]^b(n,k). (2.9)

Очевидно, b(n,k)®¥ при n®¥. Следовательно, неравенства (2.8) и (2.9) доказывают лемму, так как ряд (2.4) сходится со скоростью геометрической прогрессии со знаменателем q=1-[1-F(x)]^k<1, и, следовательно, предельное соотношение lim_n®¥nF⁽ⁿ⁺¹⁾(t)=0 выполняется (показательная функция стремится к нулю быстрее, чем степенная к бесконечности). Отметим одно важное обстоятельство - поскольку оценка (2.8) не зависит от t, то ряд (2.4) сходится на любом конечном интервале равномерно. Лемма доказана.*

Итак, условия существования функции восстановления связаны с поведением функции распределения F(t) интервалов между соседними моментами восстановления - оно не должно иметь единичного скачка в нуле, то есть исключается случай распределения, сосредоточенного в нуле.

Если не выполняется это ограничение, то можно утверждать, что процесс не развивается во времени. В самом деле, тогда при любом положительном t и k³0 имеем P{x(t)=k}=0. Следовательно, все моменты восстановления совпадают с нулем, и процесс восстановления не развивается во времени. В дальнейшем специально это условие оговаривать не будем, считая его выполненным.

Из соотношения (2.3) следует 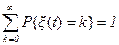при любом положительном t, поскольку (здесь считаем F⁽⁰⁾(t)=1 при t>0, поскольку t₀=0). Тогда равенство

понимается как следующее свойство процесса восстановления: на любом конечном интервале времени с вероятностью единица происходит конечное число восстановлений.

Теперь перейдем к анализу процесса восстановления с запаздыванием. Обозначим для процесса восстановления с запаздыванием, определяемого парой распределений {F₁(t),F(t)}, через H₁(t)=Mx₁(t) функцию восстановления - математическое ожидание числа восстановлений, произошедших до момента t, t³0. Тогда для нового процесса восстановления в силе остаются соотношения (2.2) и (2.3). Условия леммы относительно функции F(t) сохраняются, утверждение (2.4) сохраняется.

Чтобы отделить рассматриваемый случай от предыдущего, обозначим . Тогда равенство (2.4) принимает вид

. (2.10)

Соотношение (2.6) не меняется, только изменяется распределение случайной величины x₁, и поэтому изменяется оценка для функции

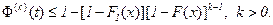
Изменение этой оценки не влияет на сходимость ряда (2.10) и на окончательные выводы. Таким образом, и для существования функции восстановления процесса восстановления с запаздыванием необходимо исключить случай единичного скачка функции распределения F(t) в нуле.

По определению дифференциал функции есть главная часть ее приращения. Для функции распределения F(x)=P{x<x} случайной величины x он с точностью до o(D) совпадает с вероятностью

P{x£x<x+D}=F(x+D)-F(x)=dF(x)+o(D) при D®0.

Введем следующие обозначения:

· A(x,D) - событие, состоящее в том, что в интервале [x,x+D) произошло восстановление,

· - событие, состоящее в том, что в интервале [x,x+D) произошло восстановление с номером n,

· B_n(x,D) - событие, состоящее в том, что в интервале [x,x+D) произошло восстановление с номером, меньшим n+1.

Очевидны соотношения

P{A_k(x,D)}=P{x£t_k<x+D}=F^(k)(x+D)-F^(k)(x)=dF^(k)(x)+ o(D).

Следовательно,

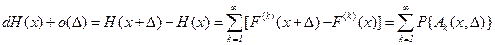. (2.11)

Если использовать равенство (2.11), то дифференциалу функции восстановления можно дать новую интересную интерпретацию.

Заметим, что при k<j справедливо включение событий . Это соотношение выполняется, так как, если в интервале [x,x+D) произошло k- ое и j- ое восстановление, то (k+1)- ое восстановление также произошло в этом интервале. Отсюда

Так как 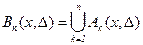, получаем двустороннюю оценку, которую можем записать с учетом двусторонней оценки для вероятности суммы событий (математическое приложение 1),

Тогда

При n®¥ получаем оценку

[1-F(D)][H(x+D)-H(x)]£ lim_n®¥ P{B_n(x,D)}=P{A(x,D)}£ [H(x+D)-H(x)]. (2.12)

Вывод. Если функция распределения F(x) непрерывна в нуле, то приращение функции восстановления в точке x или ее дифференциал можно интерпретировать как вероятность иметь восстановление (неважно какое по счету) в некоторой бесконечно малой окрестности точки x.

Поиск по сайту: