АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свойство преобразования Лапласа-Стилтьеса интеграла свертки

Читайте также:
  1. II. Элементарные преобразования. Эквивалентные матрицы.
  2. III ПРЕОБРАЗОВАНИЯ ПРИ ПОЛОВОМ СОЗРЕВАНИИ
  3. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  4. Аграрные преобразования в деревне
  5. Аддитивность интеграла Римана.
  6. Алгебраические преобразования
  7. Базовые технологии преобразования информации
  8. Билет 12 Различные уравнения прямой на плоскости, геометрический смысл параметров. Формула преобразования координат вектора при переходе к новому базису
  9. Билет 29Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования переменных.
  10. В заданиях 1-8 вычислить значение определенного интеграла.
  11. Важнейшим свойством белка является его способность к гидролизу. При этом разрушаются пептидные связи, разрушается первичная структура белка.
  12. Вещь — свойство — отношение

Для интеграла свертки двух функций распределения положительных случайных величин имеем, меняя порядок интегрирования,

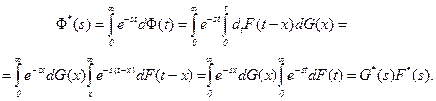
Тем самым доказано, что преобразование Лапласа-Стилтьеса интеграла свертки двух функций распределения положительных случайных величин равно произведению преобразований Лапласа-Стилтьеса этих распределений.

3. Тауберова теорема [6]

Для точной формулировки теоремы определим понятие медленно меняющейся на бесконечности функции.

Положительная функция L(x), определенная на (0,∞), называется медленно меняющейся на бесконечности, если при любом x >0

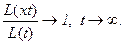
Положительная функция L(x), определенная на (0,∞), называется медленно меняющейся в нуле, если функция 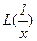является медленно меняющейся на бесконечности.

ТЕОРЕМА. Если L медленно меняется на бесконечности и то каждое из соотношений и влечет другое.

При формулировке теоремы приняты обозначения гамма–функция Эйлера.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)