АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Исследование распределения интервала, накрывающего произвольную точку

Читайте также:
  1. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  2. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  3. II. Исследование пульса, его характеристика. Места определения пульса.
  4. IIІ Исследование функций
  5. TSFSPEC (Б.Вид распределения средств.Приемник)
  6. V. Объективное исследование больного.
  7. XI.8 Принцип распределения тем курсовых работ среди студентов.
  8. Алгоритм открытого распределения ключей Диффи - Хеллмана.
  9. Алгоритм предварительного распределения ресурсов
  10. Алгоритмы распределения памяти
  11. Анализ распределения и использования прибыли предприятия
  12. Анализ распределения и использования чистой прибыли

При исследовании этого распределения можно воспользоваться свойством независимости времени перескока ξt и времени недоскока ηt для простейшего потока, доказанного в разделе (равенства (3.6) и (3.7)). Свертка распределений (3.4) и (3.5) дает при x<t

При получаем

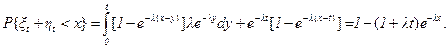
Аналогичный результат можно получить, если воспользоваться равенствами (2.45) и (2.46), полученными в главе II.

Если речь идет о бесконечно далеком моменте t, то получаем

При t<∞ для математического ожидания суммы получаем

При t→∞ для математического ожидания суммы получаем


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)