Классификация полумарковских процессов и их состояний

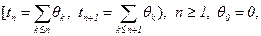Как было отмечено выше (замечание 2), полумарковский процесс в полуинтервале не меняет своих состояний, то есть можно рассматривать как время непрерывного пребывания полумарковского процесса x(t) в некотором фиксированном состоянии. В силу однородности марковского процесса восстановления (5.1) условное распределение случайной величины при условии не зависит от n. Тогда из (5.4) имеем

(5.18)

где через q обозначено время непрерывного пребывания полумарковского процесса в некотором фиксированном состоянии.

ОПРЕДЕЛЕНИЕ 1. Состояние iОE называется мгновенным, если

(5.19)

С учетом свойств полумарковского ядра 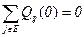из равенства (5.19) получаем для мгновенного состояния iОE равенство

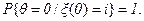
В мгновенном состоянии случайный полумарковский процесс с вероятностью единица проводит время, равное нулю.

Для мгновенного состояния из соотношения (5.9) получаем равенство при t>0

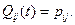
С понятием мгновенного состояния связано понятие регулярности полумарковского процесса.

Прежде всего, отметим, что считающий случайный процесс для любого t>0 определяет число состояний (число переходов), которые принимал полумарковский процесс за время t, включая момент t (случайные процессы и непрерывны справа).

ОПРЕДЕЛЕНИЕ 2. Полумарковский процесс называется регулярным, если с вероятностью единица он за конечное время совершает конечное число переходов, то есть для любого t>0 и iОE справедливо равенство

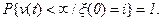
Теперь увяжем понятие регулярности с понятием мгновенности состояний.

Очевидно, что, если все состояния полумарковского процесса являются мгновенными, то за конечное время произойдет бесконечно много переходов. По-существу, эволюции такого процесса во времени не происходит, то есть такого процесса не существует. В дальнейших рассуждениях предполагаем, что все состояния полумарковского процесса не могут быть мгновенными.

ОПРЕДЕЛЕНИЕ 3. Состояние iОE называется поглощающим, если при любом конечном t

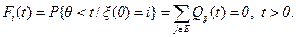(5.20)

Для поглощающего состояния i справедливо равенство

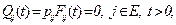(5.21)

поскольку каждое слагаемое неотрицательно,

Если произведение (5.21) равно нулю за счет того, что то распределение можно считать несобственным распределением, для которого разность трактуется как вероятность того, что случайная величина 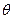принимает значение «бесконечность». В нашем случае эта разность равна единице и поэтому считаем, что, попав в поглощающее состояние i, полумарковский случайный процесс с вероятностью единица проводит в нем бесконечное время. Можно иначе интерпретировать условия Из поглощающего состояния i процесс может перейти с положительной вероятностью в какие-то состояния, но время перехода равно бесконечности. При такой интерпретации по-прежнему справедлив вывод, что, попав в поглощающее состояние i, полумарковский случайный процесс с вероятностью единица проводит в нем бесконечное время. Если произведение (5.21) равно нулю за счет того, что Как было отмечено выше, в этом случае функции можно доопределить произвольным образом. В частности, считать

При таком определении поглощающего состояния получаем, что исследуемый процесс развивается бесконечно долго.

ОПРЕДЕЛЕНИЕ 4. Полумарковский процесс называется обрывающимся, если с вероятностью единица его эволюция продолжается конечное время.

Замечание. Решение вопроса о конечном или бесконечном времени эволюции процесса зависит от конкретной реальной ситуации, которую описывает исследуемый полумарковский процесс.

Поиск по сайту: