Функция восстановления

Для функции восстановления из (2.4) следует очевидное неравенство F(t)£H(t). Для получения оценки сверху заметим, что поскольку x_k³0 и справедливо следующее соотношение между событиями

{max_{k=(1,2,...,n)}x_k<t}Ê{t_n<t},

и, следовательно, справедливо неравенство

F⁽ⁿ⁾(t)=P(t_n<t)£P{max_{k=(1,2,...,n)}x_k<t}=Fⁿ(t),

так как случайные величины x_k независимы. Поэтому из (2.4) получаем двустороннюю оценку

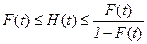. (2.54)

Оценку (2.54) можно уточнить. Воспользуемся для этого очевидным равенством

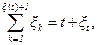
где по-прежнему обозначены x(t) число восстановлений, произошедших до момента времени t, x_t - прямое время возвращения (время перескока).

Если использовать тождество Вальда (математическое приложение 5), то получаем

M(x₁+x₂+...+x_x(t)+1)=Mx (Mx(t)+1)= Mx[H(t)+1]=t+Mx_t,

поскольку случайные величины ξ_i одинаково распределены и при i>ξ(t)+1 не зависят от ξ(t) по определению процесса восстановления.

Следовательно,

. (2.55)

Объединяя неравенства (2.54) и (2.55), получаем

. (2.56)

Поиск по сайту: