Вложенная цепь и характеристики на периоде между соседними моментами изменения состояний

В соответствии с выводами предыдущего раздела задаем матрицу интенсивностей перехода l_ij при i,jÎE, i¹j и начальное распределение вероятностей состояний, т.е. задаем некоторый однородный марковский процесс x(t).

Обозначим через 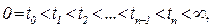неубывающую последовательность случайных соседних моментов изменения состояний марковского процесса (траектории процесса x(t) считаем непрерывными справа, x(t_n-0)¹ x(t_n)).

В дальнейшем постоянно будем придерживаться следующих обозначений

(4.16)

Так как траектории марковского процесса с дискретным множеством состояний есть ступенчатые функции, то в интервале [t_n,t_n+1) процесс не меняет состояний и принимает одно значение x_n, величина q_n есть длина этого интервала.

Вычислим для пары i,jÎE, i¹j и t>0 условную вероятность

. (4.17)

Равенство справедливо в силу однородности исследуемого марковского процесса (независимость от числа изменений состояния) и строго марковского свойства процесса x(t), так как моменты изменения состояний процесса t_n, n³0 являются марковскими моментами.

Замечание. Понятие строго марковского свойства, марковских моментов - моментов остановки и свойства строгой марковости марковского процесса с дискретным множеством состояний дано в математическом приложении 7.

Для решения этой задачи воспользуемся методом построения поглощающего экрана. Зафиксируем произвольное состояние iÎE и на том же вероятностном пространстве, на котором определен процесс x(t), построим другой однородный марковский процесс x₁(t) с тем же начальным распределением и интенсивностями перехода m_kj, которые определяются равенствами при jÎE

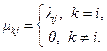(4.18)

Попав в состояние k¹i, процесс x₁(t) из него не выйдет (выход может произойти с вероятностью ноль, в состояниях k¹i построен поглощающий экран). Тогда для подмножеств элементарных событий справедливо равенство

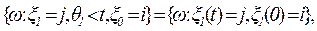
поэтому при i¹j

(4.19)

Обозначим переходные вероятности процесса x₁(t) через

Для этих вероятностей выписываем прямые уравнения Колмогорова при k,j,iÎE,

(4.20)

решение которых при начальных условиях q_kk(0)=1, q_kj(0)=0, k¹j имеет вид

(4.21)

Следовательно, при i¹j

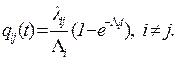(4.22)

В дальнейшем для марковского процесса полагаем l_ii=0 и Q_ii(t)=0.

Аналогичный результат (равенство (4.22)) получим, если используем обратные уравнения Колмогорова.

Если сравнить равенство (4.22) с равенством (1.11), то очевидно совпадение. Поэтому, учитывая условия, при которых получена формула (1.11), эволюцию марковского процесса можно трактовать следующим образом: в состоянии i реализуются некоторые «операции» с номерами jÎE, i¹j, длительности которых независимые экспоненциально распределенные случайные величины с параметрами l_ij. Следующий переход осуществится в состояние j, соответствующее номеру «операции» с минимальной длительностью, длительность перехода совпадает с минимумом длительностей этих операций (отметим, что такая интерпретация успешно использовалась в [3] при описании марковских систем массового обслуживания).

Из определения (4.17) и равенства (4.22) следуют равенства при любом n³0

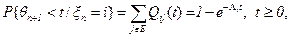(4.23)

(4.24)

(4.25)

Равенство (4.23) определяет функцию распределения времени непрерывного пребывания марковского процесса в состоянии i, точнее, распределение при условии, что это состояние равно i. Это условное распределение экспоненциальное с параметром L_i. Если вспомнить свойство отсутствия последействия экспоненциального распределения (см. параграф 1.1.), то полученный результат естественно вытекает из марковского свойства изучаемых процессов.

Равенство (4.24) определяет условное математическое ожидание времени непрерывного пребывания марковского процесса в состоянии i.

Комментируя равенство (4.25), заметим, что последовательность x(t_n)=x_n, n³0 определяет эволюцию (смену) состояний марковского процесса. В силу строго марковского свойства изучаемого процесса эта последовательность образует цепь Маркова. В самом деле, если x_n-1 характеризует прошлое, x_n определяет настоящее, а x_n+1 - будущее течение процесса, то очевидно равенство

что и доказывает марковское свойство последовательности x(t_n)=x_n. Последовательность x(t_n)=x_n называется вложенной марковской цепью. Тогда равенство (4.25) есть выражение переходных вероятностей для вложенной цепи Маркова через интенсивности перехода марковского процесса. Эта цепь имеет матрицу переходных вероятностей, у которой диагональные элементы равны нулю.

Поиск по сайту: