Индикатор

Индикатор или определяется как функция множества, принимающая два значения: ноль и единица

Если рассматривать эту функцию как функцию некоторой случайной величины ξ, то получим случайную величину, принимающую два значения и определяемую равенством

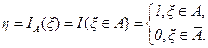
Из последнего равенства следует

7. Марковский момент. Строго марковское свойство [10]

Определение марковского момента связывается с некоторым случайным процессом . Оно устанавливает свойство независимости некоторой случайной величины от «будущего» течения процесса.

Случайный процесс определяется как мера на некотором измеримом пространстве 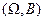. При любом множество траекторий порождает неубывающее семейство - алгебр .

Определение. Случайная величина называется марковским моментом относительно семейства , если .

Другими словами, распределение случайной величины зависит только от поведения случайного процесса до момента t.

Марковский момент называется моментом остановки, если он конечен,

Строго марковское свойство процесса с конечным множеством состояний определяется равенством

если марковский момент, и это равенство справедливо при любых

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ.. 2

ГЛАВА I. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО СВОЙСТВА 4

1.1. Определение экспоненциального распределения и его свойства. 4

1.2. Определение распределения Эрланга и его связь с экспоненциальным распределением.. 6

1.3. Определение распределения Пуассона, его свойства и связь с распределением Эрланга и экспоненциальным распределением.. 8

1.4. Распределение некоторых специальных функций от набора независимых экспоненциально распределенных случайных величин. 9

ГЛАВА II. ПРОЦЕССЫ ВОССТАНОВЛЕНИЯ.. 11

2.1. Определение процесса восстановления. 11

2.2. Функция восстановления и ее свойства. 13

2.3. Интегральные уравнения восстановления. 18

2.4. Плотность восстановления. 20

2.5. Асимптотическое поведение функции восстановления (элементарная теорема восстановления) 21

2.6. Обрывающиеся процессы восстановления. 22

2.7. Узловая теорема восстановления. 26

2.8 Характеристики случайных величин, связанных с процессом восстановления 28

1. Момент последнего на конечном интервале восстановления. 28

2. Обратное время возвращения (время недоскока) 29

3. Прямое время возвращения (перескок) 30

4. Совместное распределение прямого и обратного времен
возвращения. 31

2.9. Примеры использования узловой теоремы восстановления. 32

1. Вычисление предельных распределений прямого и обратного времен возвращения. 32

2. Вычисление предельного совместного распределения прямого и обратного времен возвращения. 33

3. Вычисление предельного распределения суммы прямого и обратного времен возвращения (распределения интервала, накрывающего бесконечно далекий момент). 34

4. Построение асимптотического разложения функции восстановления процесса восстановления с запаздыванием. 35

2.10. Некоторые полезные оценки для функций восстановления. 35

1. Функция восстановления. 36

2. Плотность восстановления. 37

3. Сравнение функций восстановления. 37

2.11. Стационарные процессы восстановления. 38

2.12. Альтернирующие процессы восстановления. 41

ГЛАВА III. ПУАССОНОВСКИЙ ПРОЦЕСС (ПРОСТЕЙШИЙ ПОТОК) 44

3.1. Определение и свойства простейшего потока. 44

3.2. Другие определения простейшего потока. 48

3.3. Исследование распределения интервала, накрывающего произвольную точку 53

3.4. Исследование условных вероятностей. 54

3.5. Исследование условных и безусловных математических ожиданий. 58

ГЛАВА IV. МАРКОВСКИЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДИСКРЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ.. 62

4.1. Определение марковского процесса. 62

4.2. Уравнения Колмогорова. 65

4.3. Вложенная цепь и характеристики на периоде между соседними моментами изменения состояний. 68

4.4. Асимптотический анализ марковских процессов. 71

4.5. Процессы размножения и гибели. 78

1. Анализ предельных характеристик. 79

2. Анализ частных случаев. 80

ГЛАВА V. ПОЛУМАРКОВСКИЕ ПРОЦЕССЫ... 85

5.1. Определение полумарковского случайного процесса. 85

1. Однородный процесс марковского восстановления и полумарковское ядро. 85

2. Определение полумарковского случайного процесса. 89

3. Примеры полумарковских процессов. 91

4. Классификация полумарковских процессов и их состояний. 92

5.2. Определение управляемого полумарковского случайного процесса 94

5.3. Определение управляемого полумарковского случайного процесса с катастрофами. 98

5.4 Определение стратегии управления и ее свойства. Постановка задачи управления и выбора оптимальной стратегии. 102

ЛИТЕРАТУРА.. 106

МАТЕМАТИЧЕСКОЕ ПРИЛОЖЕНИЕ.. 107

1. Оценки для вероятности суммы событий. 107

2. Свойство преобразования Лапласа-Стилтьеса интеграла свертки. 107

3. Тауберова теорема [6] 107

4. Различные выражения для математического ожидания. 108

5. Тождество Вальда [7] 109

6. Индикатор. 109

7. Марковский момент. Строго марковское свойство [10] 110

Поиск по сайту: