Плотность восстановления

Если при t>0 у функции восстановления существует производная H^’(t)=h(t), то ее называют плотностью восстановления. Из представлений (2.4) и (2.10) следует, что плотность восстановления существует тогда и только тогда, когда существует плотность распределений F(t)=f(t) и F₁(t)=f₁(t) при t>0. В силу того, что ряд сходится равномерно на любом конечном интервале, его можно почленно дифференцировать. Тогда из (2.4) получаем

,

где через f^(k)(t) обозначена k- кратная свертка плотности f(t).

Учитывая оценки (2.12) и равенство dH(t)=h(t)dt для дифференциалов, получаем, что функция h(t)dt есть вероятность появления восстановления в бесконечно малой окрестности точки t.

Не представляет труда получить уравнения восстановления для плотностей и их решения в терминах преобразования Лапласа-Стилтьеса. Приведем эти соотношения

, (2.21)

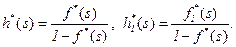
2.5. Асимптотическое поведение функции восстановления
(элементарная теорема восстановления)

Теперь исследуем асимптотическое поведение функции восстановления при t®¥.

ТЕОРЕМА 2.1. Для простого процесса восстановления при t®¥ имеет место следующее асимптотическое разложение

, (2.22)

если существует математическое ожидание и второй момент.

ДОКАЗАТЕЛЬСТВО. При доказательстве используется тауберова теорема, формулировка которой приведена в математическом приложении 3. Для того чтобы воспользоваться этой теоремой, необходимо построить разложение функции H^*(s) при s®0. В рассматриваемом случае

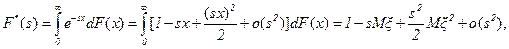
где обозначены

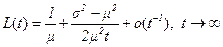, (2.23)

m= Mx, s²=Mx²-(Mx)².

Далее необходимо проверить, является ли функция L(t) медленно меняющейся на бесконечности, то есть имеет ли место равенство

при любом положительном x. Последнее равенство для функции (2.23) очевидно. Таким образом, все условия тауберовой теоремы выполняются. Следовательно, при t®¥

,

что и доказывает утверждение теоремы.*

Доказанную теорему называют элементарной теоремой восстановления и дают ее в форме следующего утверждения .

Сделаем два замечания к доказанной теореме.

Замечание 1. Почти дословное повторение доказательства для функции восстановления H₁(t) дает следующее асимптотическое разложение при t®¥

.

Из последнего равенства можно заключить, что главный член разложения не зависит от распределения F₁(t). Последнее разложение будет получено также ниже с использованием узловой теоремы восстановления.

Замечание 2. Для плотностей восстановления очевидны равенства

.

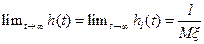Поиск по сайту: