Другие определения простейшего потока

Напомним, что в параграфе 2.1 главы II был определен случайный поток однородных событий x(t) как случайныйпроцесс, для которого область значений есть неотрицательные целые числа E={0,1,...,n,...}, x(t)ÎE, и все траектории являются неубывающими ступенчатыми функциями. Такой случайный процесс можно задать, задавая совместное распределение случайной последовательности {t_n=t_n(w), 1£n<¥}, которая определяет моменты скачков, а номер n задает номер скачка случайного процесса x(t) [5].

ОПРЕДЕЛЕНИЕ 3.2. Простейшим потоком называется всякий стационарный ординарный поток без последействия.

Приведенные определения 3.1. и 3.2. означают, что перечисленные условия стационарности, ординарности и отсутствия последействия являются необходимыми и достаточными условиями того, чтобы поток был простейшим.

Для доказательства эквивалентности этих определений необходимо доказать теперь, что из свойств стационарности, ординарности и отсутствия последействия следует, что интервалы между соседними восстановлениями (скачками потока) суть независимые экспоненциально распределенные случайные величины.

Обозначим

p_k(t)=P{x(t)=k}=P{x(t+x)-x(x)=k}=

=P{x(t+x)-x(x)=k½x(x)=n}=P{x(t+x)=k+n½x(x)=n}. (3.10)

Все эти равенства справедливы в силу выполнения свойств стационарности и отсутствия последействия (независимости приращений) процесса x(t). Как и ранее считаем P{x(0)=0}=1.

Тогда , или, обозначая имеем . Для k>0 справедливо равенство . Для любого t>0 найдется такое k>0, что и в силу монотонности функции p₀(t) получаем

При n®¥ крайние члены неравенств стремятся к . Поэтому

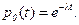(3.11)

По определению величины q выполняются неравенства 0£q£1. При q=1 вероятность появления хотя бы одного события на любом конечном интервале равна нулю, что равносильно отсутствию потока однородных событий, при q=0

на любом как угодно малом интервале будут события с вероятностью единица, а это означает, что с вероятность единица на любом конечном интервале будет сколь угодно много событий. Эти неинтересные крайние случаи из рассмотрения исключаются. Для 0<q<1 параметр l=-lnq существует и 0<l<¥.

Из условий стационарности, ординарности и отсутствия последействия вытекают следующие асимптотические равенства при D®0

(3.12)

В наших условиях по формуле полной вероятности получаем при k>0, t³0, D>0 соотношения

из которых после элементарных преобразований и перехода к пределу при D®0 получим систему дифференциальных уравнений

(3.13)

Если процесс стартует из нуля, то получаем начальные условия p₀(0)=1, p_k(0)=0, k>0, для решений системы дифференциальных уравнений (3.13).

Обозначим через производящую функцию последовательности p_k(t), k³0. Умножим k- ое уравнение (3.13) на z^k и просуммируем по k от 0 до ¥. Тогда получим

(3.14)

начальные условия определяются равенством F(0,z)=p₀(0)=1. Поэтому решение уравнения (3.14) имеет вид

lnF(t,z)-lnF(0,z)=l(z-1)

или с учетом начальных условий выписываем решение уравнения (3.14)

(3.15)

Следовательно, для искомых вероятностей получаем равенства

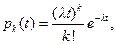(3.16)

совпадающие с равенствами (3.1).

Обозначим через x_k промежуток времени между k- м и k+1- м событием (моментом восстановления). Тогда из равенства (3.11) или (3.16) при k=0 легко выписать распределение интервала до первого восстановления

Другими словами, интервал до первого восстановления распределен по экспоненциальному закону с параметром l. Преобразование Лапласа-Стилтьеса этого распределения равно

Из равенства событий {x₀+x₁<t}={x(t)>1} следуют равенства для вероятностей

(3.17)

Преобразование Лапласа-Стилтьеса функции (3.17) равно произведению

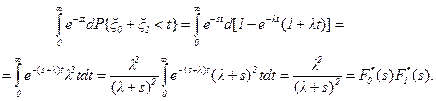(3.18)

Равенство (3.18) легко получается из равенства (1.7) при k=2 и t®¥, так как интегрируемая функция e^-(s+l)x(s+l)²x является плотность распределения Эрланга 2-го порядка с параметром (s+l). Из равенства (3.18) следует, что случайные величины x₀ и x₁ независимы и распределение x₁ экспоненциальное

Далее по индукции аналогично (3.17) и (3.18) для произвольного целого m>0 получаем

(3.19)

(3.20)

Равенство (3.20) доказывает, что последовательность {x₀,x₁,...,x_m,…} является последовательностью взаимно независимых случайных величин и

Так как это утверждение справедливо при любом k>0, то, следовательно, доказана эквивалентность определений 3.1 и 3.2.

Заметим, что равенство (3.10) определяет условные вероятности, причем эти вероятности не зависят для простейшего потока от x, n. В теории марковских процессов введенные условные вероятности называют переходными и обозначаются . Для простейшего потока имеем

.

Это же следует из равенств (3.12), которые можно считать асимптотическим разложением переходных вероятностей в окрестности нуля,

p_n,n(D)=p₀(D)=P{x(x+D)=n½x(x)=n}=1-lD+o(D),

p_n,n+1(D)=p₁(D)=P{x(t+x)=n+1½x(x)=n}=lD+o(D),

p_n,n+k(D)=p_k(D)=P{x(x+D)=k+n½x(x)=n}=o(D), при k>1. (3.21)

При этом условии свойство отсутствия последействия является марковским свойством, поскольку будущее течение процесса не зависит от его настоящего состояния. Уравнения (3.13) есть уравнения Колмогорова для переходных вероятностей или вероятностей состояний при начальном условии p₀(0)=1. Матрица интенсивностей перехода имеет вид l_n,n+1=l, l_n,n+k=0 при k>1. Поэтому справедливо

ОПРЕДЕЛЕНИЕ 3.3. Простейший поток есть однородный марковский процесс чистого размножения.

Наконец, можно для простейшего потока дать

ОПРЕДЕЛЕНИЕ 3.4. Простейший поток есть случайный процесс с однородными независимыми приращениями, которые распределены по закону Пуассона

Эквивалентность очевидно вытекает из предыдущих рассуждений, так как однородность приращений эквивалентна стационарности потока, отсутствие последействия эквивалентна независимости приращений, а ординарность следует из свойств распределения Пуассона.

В дальнейшем эти определения будут использоваться в зависимости от удобства решения конкретной задачи.

Поиск по сайту: