Определение управляемого полумарковского случайного процесса с катастрофами

Исходным объектом для конструктивного построения управляемого полумарковского процесса с катастрофами является однородная четырехмерная марковская цепь или однородный управляемый процесс марковского восстановления с катастрофами

(5.33)

Как и ранее в обозначениях (5.33) считаем:

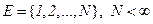· - конечное множество состояний, первая компонента однородного управляемого процесса марковского восстановления с катастрофами принимает дискретные значения из этого множества;

· – множество положительных действительных чисел, поэтому вторую компоненту и последнюю компоненту однородного управляемого процесса марковского восстановления с катастрофами отождествляем со временем, на пространстве задаем борелевскую s- алгебру[12];

· U - есть некоторое пространство управлений с s- алгеброй A подмножеств этого пространства.

Однородная марковская цепь определяется переходными вероятностями i,jОE, t,t,x,yОR⁺, BÎ A, uÎU и начальным распределением

В рассматриваемом случае предполагаем, что марковская цепь задается переходными вероятностями специального вида

в которых нет зависимости от параметров t, u и y – значений второй, третьей и четвертой компоненты на предыдущем шаге и номера шага n. Следовательно, будущее поведение однородного управляемого процесса марковского восстановления с катастрофами зависит только от значения первой компоненты и имеет место однородность этого управляемого марковского процесса восстановления. При этих дополнительных ограничениях в качестве начального распределения можно задавать константы

(5.34)

поскольку событие 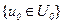являются достоверным, а относительно и 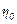далее полагаем

В дальнейшем будем использовать обозначения

(5.35)

Из равенства (5.35) следует, что можно модель усложнить и считать, что область определения функции по переменной B зависит от состояния i. Это значит для каждого iОE задано множество управлений U_i и s- алгебра A _i подмножеств этого пространства U_i. Функция , определяемая равенством (5.35), задана для i,jÎE, t,xÎR⁺, BО A _i.

Исследуем свойства функции , вытекающие из определения этой функции.

Прежде всего, заметим, что при x®Ґ получаем равенство

где функция определяется равенством (5.24) со всеми вытекающими из этого равенства свойствами.

Функции (5.35) обладают следующими свойствами при любых i,jОE,t>0,x>0 и BО A _i:

·

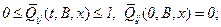
· - неубывающие по t и x, непрерывные слева функции;

·

Семейство функций порождает на измеримом пространстве (U_i, A _i) семейство вероятностных мер

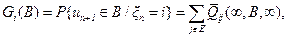iÎE, BÎ A _i. (5.36)

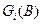Так как для любого jÎE, t,xÎR⁺, BО A _i справедливо неравенство то мера абсолютно непрерывна относительно меры и на основании теоремы Радона-Никодима существуют измеримые функции такие, для которых имеет место равенство

(5.37)

Функции есть условные вероятности

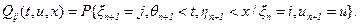(5.38)

Таким образом, однородный управляемый процесс марковского восстановления с катастрофами может быть задан семейством матриц , множеством вероятностных мер 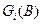и начальным распределением вероятностей состояний p_i, i,jÎE, t,xÎR⁺, uОU_i, BО A _i.

Семейство матриц будем называть полумарковским ядром управляемого полумарковского процесса с катастрофами, а семейство вероятностных мер 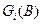будем называть семейством управляющих мер.

Из определения полумарковского ядра управляемого полумарковского процесса и полумарковского ядра управляемого полумарковского процесса с катастрофами следует предельное равенство

которое позволяет установить связь полумарковского ядра управляемого полумарковского процесса с катастрофами со стандартным полумарковским ядром.

Из равенства (5.38) следует

(5.39)

В силу монотонности функции (5.39) по переменной t получаем неравенство

(3.8)

Следовательно, мера абсолютно непрерывна относительно меры и на основании теоремы Радона-Никодима существуют измеримые функции такие, для которых имеет место равенство

(5.40)

Далее определим управляемый полумарковский процесс с катастрофами Y(t) как случайный процесс с четырьмя компонентами

(5.41)

где а считающий процесс определяется равенством (5.17).

Заметить, что процесс совпадает со стандартным полумарковским процессом, вторая компонента управляемого полумарковского процесса определяет траекторию принимаемых решений. Эта пара совпадает с управляемым полумарковским процессом X(t) (см. определение (5.32)). Третья и четвертая компоненты и принимают значения из пространства R⁺=[0,Ґ). Компоненты управляемого полумарковского процесса с катастрофами Y(t), и введенный выше считающий процесс имеют ступенчатые траектории, для которых совпадают моменты изменения состояний (изменения состояний происходят в моменты ).

Компоненты и увяжем с моментами появления некоторого события А, называемого катастрофой. Если для некоторого t>0 выполняется неравенство то считаем, что на периоде произошла катастрофа в момент . Значение процесса 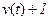определяет номер периода, на котором произошла катастрофа. Таким образом, получаем последовательность (поток) моментов катастроф при t>0. В частности, если то есть момент первой катастрофы.

Поиск по сайту: