Однородный процесс марковского восстановления и полумарковское ядро

Математическим объектом исследования является полумарковский процесс x(t) с конечным множеством состояний Без ограничения общности множество Е можно отождествить с множеством

Полумарковский процесс определяется однородной двумерной марковской цепью или однородным процессом марковского восстановления

(5.1)

Однородная марковская цепь определяется переходными вероятностями, которые будем в дальнейшем называть полумарковским ядром,

(5.2)

где и некоторым начальным распределением

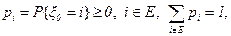(5.3)

кроме этого полагаем

Отметим, что из однородности процесса марковского восстановления следует независимость вероятностей от n. Из включения следует неотрицательность случайных величин , поэтому при tЈ0.

Нетрудно заметить, что переходная вероятность (5.1) определяет марковскую двумерную цепь специального вида, у которой будущее зависит только от первой компоненты и не зависит от второй компоненты t (вероятность не зависит от параметра t).

Из определения (5.2) получаем условное распределение случайных величин

(5.4)

в силу несовместности событий при различных j.

Для любой пары справедливо неравенство Поэтому в силу теоремы Радона-Никодима [12] существует функция , для которой выполняется соотношение . Функцию можно трактовать как условную вероятность

(5.5)

Из марковского свойства последовательности для K>0 и любых наборов следует справедливость равенства

(5.6)

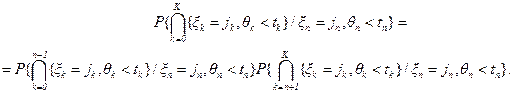
Последнее равенство формулируется как свойство марковских процессов с дискретным временем: при известном настоящем для марковского процесса с дискретным временем прошлое и будущее независимы.

При t®Ґ из определения (5.2) получаем матрицу

(5.7)

Для , для которых можно определить условную вероятность

(5.8)

и в новых обозначениях далее использовать равенство

(5.9)

Если для некоторых справедливо равенство то отношение (5.8) не определено и условное распределение нужно доопределить, например, можно считать его вырожденным распределением.

Таким образом, приходим к выводу.

Процесс марковского восстановления можно задавать тремя способами:

1. Заданием полумарковского ядра ;

2. Заданием матрицы переходных вероятностей вложенной цепи Маркова и распределениями

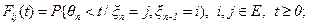
3. Заданием распределений

и

Отметим, что во всех перечисленных случаях необходимо задавать начальное распределение первой компоненты процесса марковского восстановления.

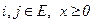Полумарковское ядро обладает при любых следующими свойствами, вытекающими из свойств вероятностей:

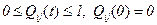· в силу того, что случайные величины q_n неотрицательные;

· - неубывающие по x, непрерывные слева функции; (5.10)

·

·

Далее обратим внимание на то, что элементы полумарковского ядра определяют поведение процесса марковского восстановления за один период (шаг) между соседними моментами изменения состояний, причем предполагается однородность переходных вероятностей (нет зависимости от номера шага n).

Определим свертку полумарковского ядра равенствами

(5.11)

Нетрудно заметить, что функция 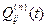определяет вероятность перехода процесса марковского восстановленияиз состояния i в состояние j за n переходов (для первой компоненты) и суммарное время меньше t (для второй компоненты).

То есть при любом n>0

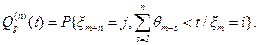(5.12)

В силу однородности процесса марковского восстановления эта вероятность не зависит от параметра m.

Далее исследуем свойства пределов Если воспользоваться леммой 2.2, доказанной в главе II, то из равенств (5.11) и (5.12) получаем при t®Ґ с учетом обозначений (5.7)

(5.13)

Равенства (5.13) доказывают, что последовательность определяющая эволюцию первой компоненты, является однородной цепью Маркова с матрицей переходных вероятностей (5.7).

Таким образом, определенная однородная цепь Маркова называется вложенной цепью Маркова. Она характеризует эволюцию первой компоненты введенной выше двумерной цепи Маркова Отметим, что выше приведенные рассуждения не ограничивают возможность перехода вложенной цепи Маркова из состояния i в то же самое состояние i. Кроме этого, следует заметить, что известная классификация цепей Маркова и их состояний [12] позволяет использовать ее в дальнейшем для классификации полумарковских процессов и их состояний.

Из марковского свойства (5.6) двумерной цепи и равенств (5.7) и (5.8) следует, что при любом K>0 и t_m>0, 0ЈmЈK

(5.14)

Последнее равенство означает, что последовательность случайных величин является условно независимой, то есть при известной траектории изменения первой компоненты совместное распределение последовательности представляется произведением условных распределений

Суммированием первого равенства (5.6) получаем совместное распределение случайных величин

(5.15)

Поиск по сайту: