Различные выражения для математического ожидания

Для действительной случайной величины ξ с функцией распределения F(x)=P{ξ<x}, - ∞<x<+∞, математическое ожидание определяется, как интеграл если интеграл сходится абсолютно. Интегрированием по частям получаем

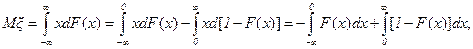
при этом заметим, что свободные члены равны нулю, так как в силу абсолютной сходимости интеграла функция распределения F(x) при x→-∞ стремится к нулю быстрее, чем x стремится к минус бесконечности, а функция 1-F(x) при x→∞ стремится к нулю быстрее, чем x стремится к бесконечности.

Для положительной случайной величины F(0)=0. Поэтому справедливо равенство

5. Тождество Вальда [7]

Тождество Вальда при определенных условиях позволяет вычислять математическое ожидание суммы случайного числа случайных слагаемых.

Пусть дана некоторая последовательность случайных возможно зависимых величин 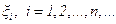, и целочисленная случайная величина ν с распределением 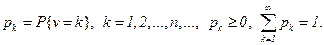Изучаются случайные величины

Случайные величины ν и могут быть зависимы.

ТЕОРЕМА (тождество Вальда). Если существуют математические ожидания 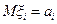и абсолютные первые моменты если ряд 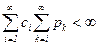сходится и выполняются условия 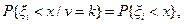при i>k, то существует математическое ожидание и справедливо тождество

ЧАСТНЫЙ СЛУЧАЙ (одинаково распределенные случайные величины ). Если выполнено условие 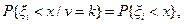при i>k, и существуют математические ожидания 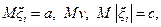то существует математическое ожидание и справедливо тождество

Поиск по сайту: