Определение стратегии управления и ее свойства. Постановка задачи управления и выбора оптимальной стратегии

ОПРЕДЕЛЕНИЕ 1. Стратегией управления называется правило выбора моментов принятия решений и правило выбора решений из заданного множества допустимых решений (управлений).

Другими словами, стратегия управления есть правило, определяющее, когда и какие решения принимаются.

Вопрос о том, когда и какие решения следует принимать, решается в зависимости от объективной информации, каковой при управлении случайным процессом является реализуемая траектория этого процесса. Если решение принимается в некоторый момент t, то значение процесса в этот момент x(t) называется настоящим процесса, траектория x(s) при 0ЈsЈt называется прошлым процесса или историей, траектория x(s) при 0ЈtЈs<Ґ называется будущим процесса.

ОПРЕДЕЛЕНИЕ 2. Если решения принимаются в некоторые заранее определенные или случайные моменты времени, то такое управление (стратегия) называется дискретным управлением.

Заметим, что дискретность управления может быть связана с тем, что управляемый процесс (объект управления) есть процесс с дискретным временем, или по самой постановке задачи управления вмешиваться в естественное течение процесса можно только в отдельные моменты времени.

ОПРЕДЕЛЕНИЕ 3. Если стратегия зависит только от истории процесса, то такая стратегия называется неупреждающей.

Для неупреждающей стратегии правило выбора решений не зависит от будущего течения управляемого процесса, а зависит от прошлого и настоящего.

ОПРЕДЕЛЕНИЕ 4. Стратегия управления называется марковской, если при принятии решений используется только информация о настоящем состоянии процесса.

Другими словами, для марковской стратегии выбор управления зависит от текущего состояния управляемого процесса и не зависит от того, каким образом в прошлом процесс попал в текущее состояние. Отметим также, что марковские стратегии являются неупреждающими.

ОПРЕДЕЛЕНИЕ 5. Стратегия управления называется однородной (стационарной), если правило принятия решений не зависит от календарного времени.

ОПРЕДЕЛЕНИЕ 6. Стратегия управления называется рандомизированной, если в процесс принятия решений введен случайный эксперимент, который определяется некоторой вероятностной мерой, построенной на измеримом пространстве допустимых управлений.

ОПРЕДЕЛЕНИЕ 7. Стратегия управления называется детерминированной (нерандомизированной), если вероятностная мера, построенная на измеримом пространстве допустимых управлений, является вырожденной.

Заметим, что множество детерминированных стратегий является собственным подмножеством множества рандомизированных стратегий, поскольку вырожденные распределения являются частным случаем распределений.

Приведенные выше определения формулируют свойства стратегий.

ПРИМЕР. В заключение настоящего параграфа исследуем свойства стратегий, определенных выше для управляемого полумарковского процесса.

В соответствии с определением управляемый полумарковский процесс задается полумарковским ядром (5.29) и семейством вероятностных мер 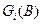(5.27), i,jÎE, tÎR⁺, uОU_i, BО A _i. Меры 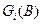, iÎE, BО A _i, определенные на измеримых пространствах управлений (U_i, A _i), задают стратегию управления (правило выбора решений). Следовательно,

· стратегия является марковской, поскольку распределения 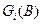зависят только от текущего состояния i;

· стратегия является однородной, поскольку распределения 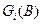не зависят только от времени;

· стратегия, определяемая распределениями 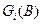, является рандомизированной, поскольку в процесс принятия решения введен случайный эксперимент.

Таким образом, в описанной выше модели управляемого полумарковского процесса рассматривается класс однородных марковских рандомизированных стратегий (отметим так же, что в этой модели речь идет о дискретном управлении, так как решения принимаются в моменты изменения состояний первой компоненты управляемого полумарковского процесса).

Следует заметить, что при фиксированной стратегии получаем фиксированный управляемый полумарковский случайный процесс. Если задается множество стратегий управления, то получаем множество управляемых полумарковских случайных процессов. Для этого случая, когда имеем множество управляемых случайных процессов, можно ставить задачу выбора наилучшего в каком-то смысле случайного процесса, то есть выбора наилучшей (оптимальной) стратегии управления. Для строгой постановки оптимизационной задачи необходимо определить цели управления, то есть определить в каком смысле одна стратегия лучше другой.

ЛИТЕРАТУРА

1. Бочаров П.П., Печинкин А.В. Теория вероятностей, Математическая статистика. Москва. Гардарика, 1998.

2. Б.В.Гнеденко, И.Н.Коваленко. «Введение в теорию массового обслуживания», URSS, Москва, 2005 год.

3. Ивченко Г.И., Каштанов В.А., Коваленко И.Н. Теория массового обслуживания. М., Высшая школа, 1982.

4. Д.Кокс и В.Смит. «Теория восстановления», Советское радио, Москва, 1967

5. А.Я.Хинчин. «Работы по математической теории массового обслуживания». Физ.-матгиз, Москва, 1963 год.

6. В.Феллер. «Введение в теорию вероятностей и ее приложения» (том 2), Мир, Москва, 1967 год. (тауберовы теоремы, теорема восстановления)

7. А.Н.Колмогоров. О суммах случайного числа случайных слагаемых. Избранные труды. А.Н.Колмогоров «Теория вероятностей и математическая статистика», Наука, 1986.

8. В.С.Королюк и др. «Справочник по теории вероятностей математической статистике». Москва, Наука, 1985.

9. С.Карлин. Основы теории случайных процессов. Мир, Москва, 1971.

10. Математическая энциклопедия. Том 3. Издательство «Советская энциклопедия», Москва, 1982.

11. А.Н.Колмогоров. К вопросу о дифференцируемости переходных вероятностей в однородных по времени процессах Маркова со счетным множествам состояний. Избранные труды. А.Н.Колмогоров «Теория вероятностей и математическая статистика», Наука, 1986.

12. А.Н.Ширяев. Вероятность 1,2. Москва, МЦНМО, 2004.

13. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды.

Специальные функции.- М.: Наука, 1983.

Поиск по сайту: