Асимптотический анализ марковских процессов

Асимптотический анализ марковских процессов с непрерывным временем и дискретным множеством состояний состоит в исследовании характеристик процесса при t®¥. Отметим, что при этом исследовании определяющую роль будут играть асимптотические свойства вложенной марковской цепи, а доказательства предельных теорем будут опираться на предельные теоремы теории восстановления.

Зафиксируем j,iÎE и положим P{x₀=i}=1, т.е. считаем, что почти все траектории процесса x(t) выходят из состояния i. Введем в рассмотрение момент времени t первого попадания процесса в состояние j

и обозначим В силу однородности процесса имеем равенство при n>0

(4.26)

Если i=j, то последовательность соседних моментов попадания процесса x(t) в состояние j образует простой процесс восстановления. У этого процесса восстановления интервалы между соседними моментами восстановления x_jj^(k), k=1,2,...(k- номер интервала) имеют распределение

Доказательство этого факта (независимость случайных величин x_jj^(k) при различных k и независимость распределения P{x_jj^(k)<t} от номера k, то есть факт, что это последовательность одинаково распределенных величин) следует из однородности процесса и того, что моменты изменения состояний марковского процесса с дискретным множеством состояний являются моментами остановки.

Заметим, что из определения интервалов x_jj^(k), k>0 следует, что каждый из них состоит из двух частей - периода, когда процесс x(t) пребывает в состоянии j, и периода, когда он пребывает в других состояниях.

Если i¹j, то последовательность соседних моментов попадания процесса x(t) в состояние j образует процесс восстановления с запаздыванием, у которого интервалы между соседними моментами восстановления x_ij⁽¹⁾=x_ij, x_jj^(k), k=2,3,...(k- номер интервала) имеют соответственно распределения

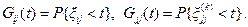(4.27)

Это также следует из однородности и строго марковского свойства исследуемого процесса.

Исследуем распределения G_ij(t), i,jÎE. Прежде всего, заметим, что интервалы x_ij представляют собой сумму случайного числа зависимых (связанных в цепь Маркова) слагаемых, распределенных по экспоненциальному закону с разными параметрами. Поэтому можно утверждать, что распределения G_ij(t), i,jÎE непрерывны. Далее по формуле полной вероятности с учетом равенства (4.22) получаем (в тех же обозначениях) систему интегральных уравнений

(4.28)

Отметим, что при i=j первое слагаемое в (4.28) равно нулю в силу принятого выше допущения l_ii=0 и равенства

Обозначим тогда из (4.28) следует

(4.29)

Таким образом, получили соотношения для функций распределения, полностью определяющих введенные процессы восстановления.

Обозначим через

математическое ожидание времени перехода марковского процесса из состояния i в состояние j. Интегрированием уравнений (4.29) получаем систему алгебраических уравнений для математических ожиданий T_ij

или

(4.30)

если использовать обозначения (4.24) и (4.25). Очевидно равенство (4.30) можно получить, если использовать формулу полного математического ожидания.

Предположим далее, что для вложенной цепи Маркова существует стационарное распределение вероятностей состояний

Из определения стационарного распределения следуют равенства

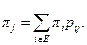
Умножим равенство (4.30) на p_i и просуммируем по iÎE. Получаем

или

Отсюда получаем

(4.31)

Соотношение (4.30) связывает математическое ожидание времени возвращения марковского процесса со стационарными характеристиками вложенной цепи и математическими ожиданиями времен непрерывного пребывания в каждом состоянии.

Далее исследуем свойства этих процессов восстановления в зависимости от свойств вложенных цепей Маркова.

ТЕОРЕМА 4.3. Если для марковского процесса с конечным или счетным множеством состояний Е вложенная цепь Маркова имеет один класс существенных состояний Е₀ и это класс возвратных состояний, то при jÎE₀ и любых iÎE последовательность {x_ij, x_jj^(k), k=2,3,... } является необрывающимся процессом восстановления, при jÎE\E₀ и любых iÎE последовательность {x_ij,x_jj^(k),k=2,3,... } является обрывающимся процессом восстановления.

ДОКАЗАТЕЛЬСТВО. Для доказательства теоремы достаточно воспользоваться результатами, изложенными в главе II «Процессы восстановления» и показать, что распределения (4.27) являются собственнымипри jÎE₀ и любых iÎE, и являются несобственнымипри jÎE\E₀ и любых iÎE. С другой стороны, если использовать теоремы 2.1. и 2.2. главы II, то можно утверждать, что свойства обрыва или необрыва процесса восстановления однозначно определяются поведением функции восстановления при t®¥. Если этот предел ограничен, то процесс восстановления обрывается, если не ограничен, то процесс не обрывается.

Воспользуемся этим критерием для доказательства теоремы.

Обозначим через H_ij(t) функцию восстановления процесса восстановления {x_ij,x_jj^(k),k=2,3,...}. По определению, функция восстановления есть математическое ожидание числа восстановлений (попаданий марковского процесса в состояние j), произошедших до момента t.

В дальнейших рассуждениях воспользуемся критериями возвратности [12]. Если состояние j - невозвратно, jÎE\E₀, то вероятность возвращения f_jj<1 и для любого iÎE вероятность f_ij£1, где f_ij - вероятностьрано или поздно из состояния i попасть в состояние j. Это следует из определения невозвратности [12]. Тогда математическое ожидание числа восстановлений (возвращений) за бесконечное время ограничено и равно

(4.32)

так как Таким образом, при jÎE\E₀ получаем обрывающийся процесс восстановления.

Если сравнить формулы (4.32) и (2.25) принять обозначения , то при i=j получим равенство если состояние j - невозвратно, jÎE\E₀.

Если состояние j - возвратно, jÎE₀, то вероятность возвращения f_jj=1 по определению. В силу того, что вложенная цепь Маркова имеет один класс существенных состояний и эти состояния возвратны, то для любого iÎE вероятность f_ij=1. Поэтому математическое ожидание числа восстановлений за бесконечное время неограниченно, H_ij(t)®¥ при t®¥. В этом случае получаем необрывающийся процесс восстановления.*

Замечания.

1. Не представляет труда обобщить теорему на случай нескольких существенных классов возвратных состояний (по-прежнему, при условии отсутствия существенных невозвратных состояний). Если начальное состояние i и состояние j принадлежат одному классу, то процесс восстановления будет необрывающимся. Если начальное состояние i принадлежит множеству несущественных состояний, а состояние j принадлежат некоторому классу существенных возвратных состояний, то процесс восстановления будет необрывающимся, если вероятность перехода из несущественных состояний в этот класс равна единице. Во всех остальных случаях процесс будет обрываться.

2. Если вложенная цепь состоит из несущественных состояний и поглощающих состояний или множества существенных невозвратных состояний, то в этих случаях вложенные процессы восстановления будут обрывающимися.

ТЕОРЕМА 4.4. Если для марковского процесса с счетным множеством состояний Е вложенная цепь Маркова имеет один класс существенных состояний Е₀, это класс возвратных положительных состояний и существует для вложенной цепи стационарное распределение вероятностей состояний, то существуют пределы и для этих пределов справедливы соотношения

при jÎE₀ и любых iÎE,

p_j=0 при jÎE\E₀ и любых iÎE. (4.33)

ДОКАЗАТЕЛЬСТВО. Для фиксированных j,iÎE введем в рассмотрение процесс восстановления {x_ij,x_jj^(k),k=2,3,...}, функцию восстановления которого обозначим через H_ij(t). Функции распределения G_ij(t)=P{x_ij<t} непрерывны в нуле, поэтому, если учесть вероятностную интерпретацию для функции восстановления, которая обсуждалась в разделе 2.2., то по формуле полной вероятности можно записать

при i¹j,

(4.34)

Поскольку для рассматриваемого случая выполняются условия теоремы 4.3, то при jÎE₀ введенный процесс восстановления будет необрывающимся. Поэтому можно воспользоваться узловой теоремой восстановления (параграф 2.7.) и получить (нерешетчатость следует из непрерывности распределений G_ij(t), T_jj<¥ в силу положительности состояния j)

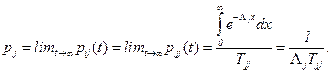
С учетом равенств (4.24) (4.31) получаем утверждение теоремы.

Если jÎE\E₀, то в силу теоремы 4.3 процесс восстановления будет обрывающимся и в силу следствия 2.1 (параграф 2.2) пределы (4.34) равны нулю, так как .*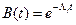

Замечания.

1. Для марковской цепи с конечным множеством состояний все существенные состояния положительно возвратны. Поэтому для такой вложенной цепи условия теоремы 4.4. сводятся только к наличию одного класса существенных сообщающихся состояний.

2. В условиях теоремы нет ограничений на периодичность вложенной цепи Маркова. Цепь может быть периодичной, d>1.

Далее заметим, что при любом начальном распределении , имеем равенство

Поэтому из существования пределов следует существование пределов

Теперь, используя уравнения Колмогорова (4.12) или (4.14), получим уравнения для пределов Для этого в (4.12) перейдем к пределу при t®¥. Правая часть стремится к константе 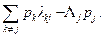Следовательно, левая часть (4.12) также стремится к константе, причем в силу ограниченности вероятности p_ij(t), 0£ p_ij(t)£1 при любых t>0, предел производной может быть только нулем. Отсюда получаем систему алгебраических уравнений для предельных вероятностей состояний марковского процесса

(4.35)

Поиск по сайту: