АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Простейшие случаи интегрируемости уравнения Эйлера

Читайте также:
  1. I I. Тригонометрические уравнения.
  2. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  3. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  4. V2: Применения уравнения Шредингера
  5. V2: Уравнения Максвелла
  6. VI Дифференциальные уравнения
  7. Алгебраические уравнения
  8. Алгебраические уравнения
  9. Алгоритм составления уравнения химической реакции
  10. АНАЛИЗ УРАВНЕНИЯ (13)
  11. Аналитическое решение данного дифференциального уравнения
  12. Аналитическое решение данного дифференциального уравнения

1. не зависит от .

В этом случае уравнение Эйлера имеет вид

. (6)

Решение этого дифференциального уравнения не содержит элементов произвола и поэтому, вообще говоря, не удовлетворяет граничным условиям , .

Лишь в исключительных случаях, когда кривая (6) проходит через граничные точки и 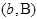существует кривая, на которой может достигаться экстремум.

2. зависит от линейно, то есть, .

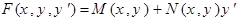Уравнение Эйлера в этом случае имеет вид:

. (7)

 

Полученное уравнение, как и в случае (1), является конечным, а не дифференциальным уравнением. Кривая, определяемая уравнением , вообще говоря, не удовлетворяет граничным условиям, и, значит, вариационная задача, как правило, не имеет решения в классе непрерывных функций. Если в некоторой области C плоскости , то выражение является полным дифференциалом и функционал

не зависит от пути интегрирования: значение функционала одно и тоже на допустимых кривых. Вариационная задача теряет смысл.

3. зависит лишь от , то есть .

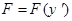Уравнение Эйлера имеет вид

.

В этом случае экстремалями являются прямые всевозможные линии

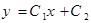, (8)

где и 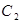- произвольные постоянные.

4. не зависит от , то есть .

В этом случае уравнение Эйлера , откуда

(9)

где - произвольная постоянная.

Уравнение (9) есть дифференциальное уравнение первого порядка. Интегрируя его, находим экстремали задачи.

5. F не зависит явно от , то есть .


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)