АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основная задача вариационного исчисления

Читайте также:
  1. I. 3.1. Двойственная задача линейного программирования
  2. I. Основная форма: помешательство.
  3. II Основная часть
  4. II. ОСНОВНАЯ ЧАСТЬ (»70 мин)
  5. II. Основная часть.
  6. II.2. Задача о назначениях
  7. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  8. III. Основная часть
  9. V. ОСНОВНАЯ ПРАКТИКА ЯСНОГО СВЕТА
  10. VI. Общая задача чистого разума
  11. Билет 5 Теорема Безу и следствия из неё. Основная теорема алгебры.
  12. Бухгалтерский баланс – основная форма бухгалтерской отчетности.

Лабораторная работа №10

Тема: Простейшая задача Вариационного исчисления. Уравнение эйлера

 

Цель работы: Ознакомиться с простейшей задачей вариационного исчисления и уравнением Эйлера, овладеть методикой решения экстремальных задач в функциональных пространствах.

 

Основная задача вариационного исчисления

Пусть функция имеет непрерывные частные производные по всем аргументам до второго порядка включительно. Среди всех функций y(x), имеющих непрерывную производную и удовлетворяющих граничным условиям:

y(a)=A, y(b)=B. (1)

Найти функцию, которая доставляет слабый экстремум функционалу

. (2)

Другими словами, простейшая задача вариационного исчисления состоит в отыскании слабого экстремума функционала вида (2) на множестве всех гладких кривых, соединяющие две заданные точки P1(a, A) и P2(b, B).

Теорема 1. Для того чтобы функционал (2), определённый на множестве функций y=y(x), имеющих непрерывную первую производную, и удовлетворяющих граничным условиям (1), достигал на заданной функции y(x) экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера:

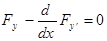. (3)

Интегральные кривые уравнения Эйлера называют экстремалями (лагранжевыми кривыми). Уравнение Эйлера в развёрнутом виде:

(4)

 

Уравнение (4) представляет собой дифференциальное уравнение второго порядка, так что его общее решение должно зависеть от двух произвольных постоянных. Значения этих постоянных, вообще говоря, определяются из граничных условий (1).

Экстремум функционала (2) может реализоваться только на экстремалях, которые удовлетворяют условиям (1).

Краевая задача:
(5)

не всегда имеет решение, а если решение существует, то оно может быть не единственным.

Пример 1. Найти экстремали функционала

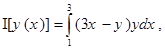
удовлетворяющие граничным условиям

.

Решение. Уравнение Эйлера имеет вид 3x-2y=0, откуда y(x)=3/2 x . Так как экстремаль не удовлетворяет условию , то данная вариационная задача решения не имеет.

 

Пример 2. Найти кривые, на которых может достигать экстремума функционал
.

Решение. Здесь , так что уравнение Эйлера имеет вид . Общее решение уравнения Эйлера есть . Граничные условия дают систему линейных уравнений для определения и .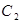

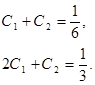
Отсюда . Следовательно, экстремум может достигаться лишь на кривой .

Пример 3. Найти экстремали функционала

удовлетворяющие граничным условиям , .

Решение. Уравнение Эйлера имеет вид , его общим решением является . Используя граничные условия, получим , где - произвольная постоянная.

Таким образом, поставленная задача имеет бесчисленное множество решений.

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)