Итерация 1

1) Проверка критерия оптимальности. Если в последней строке симплекс-таблицы нет отрицательных значений, то получено оптимальное решение. В нашем примере значения, расположенные в последней строке симплекс-таблицы в столбцах переменных x 1 и x 2 отрицательны. Поэтому эта таблица не определяет оптимального плана.

2) Определение новой базисной переменной. Отрицательные значения в последней строке показывают, что производства обоих продуктов являются прибыльными и единица первого продукта увеличивает выручку на 40, а единица второго продукта – на 100. Поэтому следует вводить в базис одну из переменных x 1 или x 2. Выберем x 2 в качестве новой базисной переменной, т.е. вводим в базис производство второго продукта. Соответствующий переменной x 2 столбец назовем ведущим столбцом (в таблице этот столбец выделен).

3) Определение новой свободной переменной. Для определения новой свободной переменной составим отношения столбца значений базисных переменных (второго столбца) к положительным элементам ведущего столбца и найдем среди них минимальное:

.

Так как минимальное значение достигается на втором отношении, то базисная переменная s 2 переходит в свободные. Вторую строку назовем ведущей (в таблице эта строка выделена). Число на пересечении ведущей строки и ведущего столбца назовем ведущим элементом.

4) Пересчет симплекс- таблицы. Теперь для нового базиса s 1, x 2 составим новую симплекс-таблицу (табл.2.1.2). Ее можно получить из старой симплекс-таблицы следующим образом. Все элементы ведущей (второй) строки, разделенные на ведущий элемент 0,3, образуют вторую строку новой таблицы. Например, элементу второй строки 25 первой симплекс-таблицы будет соот-ветствовать элемент второй строки новой симплекс- таблицы .

Остальные элементы новой таблицы получаются из соответствующих элементов старой таблицы. Каждому элементу соответствует один элемент в ведущей строке и один элемент в ведущем столбце. Используя эти элементы, формулы для пересчета можно сформулировать следующим образом:

Приведем пример пересчета элемента 1 000 в первой строке. Заметим, что пересчитываемому элементу 1000 соответствуют элемент 10 ведущего столбца и элемент 25 в ведущей строке. Тогда элементу 1 000 соответствует элемент в новой таблице:

.

Аналогично пересчитывается последняя строка. Например, первому элементу 0 последней строки соответствует элемент 25 в ведущей строке и элемент -100 в ведущем столбце. Тогда первый элемент последней строки новой таблицы будет равен:

.

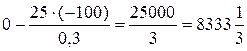Таблица 2.1.2

Базис	Значение	x 1	x 2	s 1	s 2
s 1=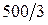
x 2=
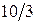
z
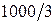
		Δ1	Δ2	y 1	y 2

Симплекс-таблица определяет новый базисный план. Значения во втором столбце определяют значения базисных переменных s 1 = 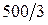, x 2 = .

Все переменные, не входящие во второй столбец, являются свободными и поэтому равны 0: x 1 = s 2 = 0.

Таким образом, новое базисное решение прямой задачи имеет вид:

X 1 ={ x 1=0, x 2= , s 1= 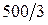, s 2=0}

Последняя строчка определяет:

- значение целевой функции прямой задачи Z = ;

- значение Δ1= в столбце x 1 означает, что производство первого продукта прибыльно;

- значение Δ2 = 0 в столбце x 2 означает, что производство второго продукта рентабельно;

- значение 0 в столбце s1 означает, что теневая цена 1 кг сырья равна y 1=0,

- значение 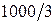в столбце определяет y 2 теневую цену 1 часа работы оборудования.

Заметим, что значение целевой функции двойственной задачи

W = 1000∙0 + 25∙ 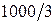= равно значению целевой функции прямой задачи.

Поиск по сайту: