 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Логарифмическая функция
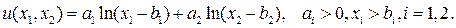
Пример 6.1.1
Пусть потребитель определил отношение предпочтения для наборов из двух товаров X = (x 1, x 2), состоящего из x 1кг. яблок и x 2 кг. конфет. Допустим, что для него строго предпочтительнее набор, в котором одновременно больше и яблок и конфет.
Допустим, что потребителю безразличны наборы
X = (1,1) (из 1 кг яблок и 1 кг конфет),
Y= (2, 2/3) (из 2 кг яблок и 2/3 кг конфет)
т.е. 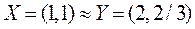 .
.
Набор Y= (2, 2/3) строго предпочтительнее набора Z = (1, 1/2) т.е. для потребителя приобрести 2 кг яблок и 2/3 кг конфет строго предпочтительнее, чем приобрести 1 кг яблок и 1/2 кг конфет. Тогда аксиома транзитивности означает, что для потребителя набор товаров X строго предпочтительнее набора товаров Z:
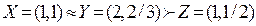
т.е. приобрести 1 кг яблок и 1 кг конфет, строго предпочтительнее, чем приобрести 1 кг яблок и 1/2 кг конфет.
Функцию полезности для данного примера можно построить, например,следующим образом. Обозначим b 1 = 50 ден. ед. стоимость 1 кг. яблок, а – b 2 = 150 ден. ед. стоимость 1 кг. конфет. Допустим, что полезность набора товаров целиком определяется его стоимостью. В этом случае в качестве функции полезности набора X = (x 1, x 2) можно принять стоимость товаров, входящих в этот набор:
u (x 1, x 2) =50 x 1 + 150 x 2.
Вычислим полезность всех рассмотренных выше наборов:
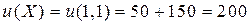 ден.ед.
ден.ед.
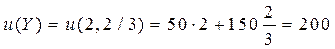 ден.ед.
ден.ед.
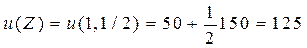 ден.ед.
ден.ед.
Следует заметить, что полезность набора товаров не всегда совпадает с его стоимостью. Например, для потребителя с повышенным сахаром полезность яблок несомненно выше полезности конфет.
Поиск по сайту: