Решения этой задачи в ЭТ

Установим начальные значения х ₁ и х ₂, равными 1. Таблица с начальными значениями х ₁ и х ₂ в режиме вычислений приведена в табл. 4.2.1, в режиме формул – табл. 4.2.2.

В ячейку D7 введем формулу для вычисления целевой функции (4.2.3):

= B4*B4 + C4*C4 + 4*B4. В ячейку D9 введем формулу левой части неравенства (4.2.4): = СУММПРОИЗВ(B4:C4;B9:C9). В ячейку F9 – значение правой части ограничения (4.2.4): 200.

Таблица 4.2.1

Таблица 4.2.2

Для вычисления минимального значения целевой функции воспользуемся режимом Поиск решения. Для этого:

- выполнить команды: Серви с 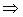Поиск решения. Откроется диалоговое окно Поиск решения;

- заполнить поля целевой ячейки и изменяемые ячейки (рис. 4.2.1);

- для ввода ограничений щелкнуть по кнопке Добавить. Появится окно Добавление ограничений. Ввести ограничения (4.2.4) – D9 ≥ F9. Нажать на кнопку ОК;

- для ввода параметров щелкнуть по кнопке Параметры. Появится окно Параметры поиска решения (рис. 4.2.2). Курсором мыши поставить флажки Неотрицательные значения и квадратичная;

- Для запуска режима Поиск решения нажать кнопку Выполнить.

В результате получаем решение задачи (табл. 4.2.3).

Из него следует, что минимальное значение целевой функции 20 398 достигается при значениях

x 1 = 99, x 2 =101.

Вопросы для самопроверки

1. Может ли целевая функция квадратичного программирования содержать ?

2. Могут ли ограничения задачи квадратичного программирования содержать ?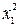

3. Является ли следующая задача задачей квадратичного программирования +sin x

при ограничениях x ₁+ x ₂ ≥ 200, x ₁ ≥ 0, x ₂ ≥ 0?

Рис. 4.2.1

Рис. 4.2.2

Таблица 4.2.3

Поиск по сайту: