 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Выполнение задания 1
Рассмотрим реализациюалгоритма симплекс-метода на примере.
Пример 1.1
Для производства двух видов продукции фирма использует два вида ресурсов: ресурс 1 – сырье, ресурс 2 – время изготовления продукции на оборудовании. Запасы ресурсов ограничены: в день может быть использовано не более 1 000 кг сырья и суммарное время работы оборудования не превосходит 25 часов. Нормы затрат каждого ресурса на единицу каждого продукта и рыночные цены заданы в табл. 1.1
Таблица 1.1
| Ресурс | Нормы затрат на ед. продукции | Запас ресурса | |
| продукт 1 | продукт 2 | ||
| сырье | a 11 =5 | a 12 =10 | b 1=1000 |
| время изготовления | a 21 =0,1 | a 22 =0,3 | b 2=25 |
| цена за ед. продукции | c 1=40 | c 2 =100 |
Требуется найти план выпуска продукции, который обеспечивает максимальную стоимость реализации (выручку).
Обозначим:
x 1 – план выпуска продукции 1,
x 2 – план выпуска продукции 2,
s 1 – остаток от производства ресурса 1,
s 2 – остаток от производства ресурса 2.
Запишем каноническую форму задачи (1.1.10 – 1.1.12):
найти план x 1, x 2, s 1, s 2, который дает максимальную выручку
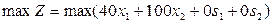
при ограничениях:
 ,
,
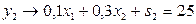 ,
,
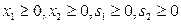 .
.
Решение
3.1.1. Построение начального базисного плана
Пусть в начальном базисном плане
x 1, x 2 – свободные переменные (т.е. x 1= x 2=0), а
s 1 =1000 и s 2=25 базисные переменные.
В симплекс-методе удобно использовать симплекс-таблицы.
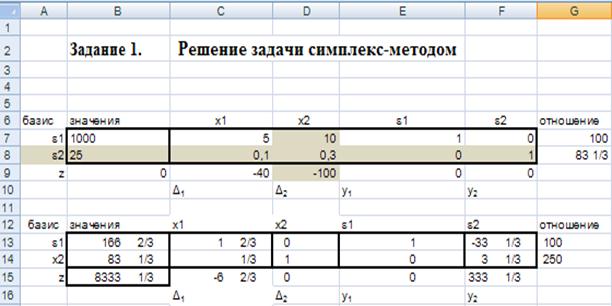
Рассмотрим построение первой симплекс-таблицы для выбранного начального базисного решения. В ячейки С7:С8 введем числовые значения 1 000 и 25 базисных переменных s 1 и s 2. Остальные столбцы состоят из коэффициентов перед переменными x j в левых частях ограничений (1.1.11), (1.1.12). Последняя строка симплекс-таблицы состоит из значений целевой функции Z = 0 и коэффициентов целевой функции Z.
Переход от одного базисного плана к другому сопровождается преобразованием симплексных таблиц. Такой переход называется итерацией.
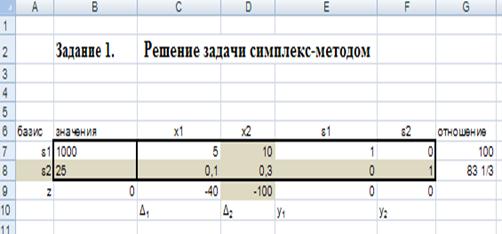
3.1.2. Итерация 1. Каждая итерация состоит из нескольких действий.
1) Проверка критерия оптимальности. Если в последней строке симплекс-таблицы нет отрицательных значений, то получено оптимальное решение. В нашем примере значения, расположенные в последней строке симплекс-таблицы в столбцах переменных x 1 и x 2 отрицательны. Поэтому эта таблица не определяет оптимального плана.
2) Определение новой базисной переменной. Отрицательные значения в последней строке показывают, что производства обоих продуктов являются прибыльными и единица первого продукта увеличивает выручку на 40, а единица второго продукта – на 100. Поэтому следует вводить в базис одну из переменных x 1 или x 2. Выберем x 2 в качестве новой базисной переменной, т.е. вводим в базис производство второго продукта. Соответствующий переменной x 2 столбец назовем ведущим столбцом (в таблице этот столбец выделен).
3) Определение новой свободной переменной. Для определения новой свободной переменной составим отношения столбца значений базисных переменных (второго столбца) к положительным элементам ведущего столбца и найдем среди них минимальное значение.
· В ячейку G7 введем формулу =B7/D7 и ячейку G8 введем формулу =B8/D8.
Так как минимальное значение достигается в ячейку G8, то базисная переменная s 2 переходит в свободные. Вторую строку назовем ведущей (в таблице эта строка выделена). Число на пересечении ведущей строки и ведущего столбца назовем ведущим элементом.
4) Пересчет симплекс-таблицы. Теперь для нового базиса s 1, x 2 составим новую симплекс-таблицу. Ее можно получить из старой симплекс-таблицы следующим образом.
Все элементы ведущей (второй) строки, разделенные на ведущий элемент 0,3, образуют вторую строку новой таблицы. Например, элементу второй строки 25 первой симплекс- таблицы будет соответствовать элемент второй строки новой симплекс- таблицы  .
.
• Для пересчета этого элемента в ячейку B14 введем формулу =B8/$D8$
и скопировать эту ячейку в C14:F14.
Остальные элементы новой таблицы получаются из соответствующих элементов старой таблицы. Каждому элементу соответствует один элемент в ведущей строке и один элемент в ведущем столбце. Используя эти элементы, формулы для пересчета можно сформулировать следующим образом:
| новый элемент | = старый элемент - | (элемент ведущего столбца)·(элемент ведущей строки) |
| ведущий элемент |
Приведем пример пересчета элемента 1 000 в первой строке. Заметим, что пересчитываемому элементу 1000 соответствуют элемент 10 ведущего столбца и элемент 25 в ведущей строке. Тогда элементу 1 000 соответствует элемент в новой таблице:
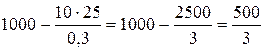 .
.
· Для пересчета этого элемента в ячейку B13 введем формулу
=B7-B8*$D$7/$D8$ и скопировать эту ячейку в C13:F13.
Аналогично пересчитывается последняя строка. Например, первому элементу 0 последней строки соответствует элемент 25 в ведущей строке и элемент -100 в ведущем столбце. Тогда первый элемент последней строки новой таблицы будет равен:
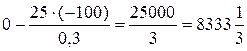 .
.
· Для пересчета этого элемента в ячейку B15 введем формулу
=B9-B8*$D$9/$D8$ и скопировать эту ячейку в C15:F15.
В результате пересчета получили новую симплекс-таблицу и переходим ко второй итерации.
Поиск по сайту: