Пример 5.1.2

Допустим, что стоимость выпуска продукции Y связана со стоимостью затрат труда L и основных фондов K по формуле

Пусть стоимость основных фондов равна K = 640 000 = 8² 100² руб., а стоимость фонда заработной платы – L = 810 000 = 3⁴ 10⁴ руб. Тогда стоимость выпуска продукции Y составит

Предельные производительностиресурсов

Производственная функция удовлетворяет свойству монотонности, если из неравенств

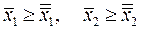
следует неравенство

(5.1.5)

Свойство монотонности означает, что увеличение затрат любого ресурса не приводит к уменьшению выпуска продукции.

Если производственная функция дифференцируема по всем аргументам, то свойство монотонности означает, что частные производные являются неотрицательными

(5.1.6)

Частная производная называется предельной производительностью 1-го ресурса. Аналогично, частная производная называется предельной производительностью 2-го ресурса. Предельная производительность ресурса показывает, на сколько единиц изменяется выпуск продукции при возрастании ресурса на единицу. Пусть затраты ресурса 1 изменяются на величину 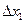, а затраты ресурса 2 – на величину . Тогда формула

определяет приращение выпуска, вызванное приращением ресурсов.

Из дифференциального исчисления следует, что приращениевыпуска можно приблизительно равно полному дифференциалу

(5.1.7)

В частности, если затраты ресурса 1 изменяются на величину 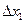, а затраты ресурса 2 не изменяются т.е. 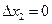, то приращениевыпуска приблизительно равно

(5.1.8)

Аналогично, если затраты ресурса 1 не изменяется = 0, а затраты ресурса 2 изменяется на величину 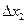, то приращение выпуска приблизительно равно

(5.1.9)

Поиск по сайту: