Найдем границы интервала устойчивости первого ресурса

Заметим, что при уменьшении запаса сырья на 200 ( Δ b 1 = -200) выпуск первой продукции становится отрицательным x 1= 100 + 0,6 Δ b 1 = -20.

Это означает, что такое изменение выводит запас ресурса за интервал устойчивости.

Изменение запаса сырья на величину Δ b 1 будет допустимым, если оптимальная программа выпуска будет неотрицательна, т.е. выполняются неравенства x 1= 100 + 0,6 Δ b 1 ≥ 0, x 2 = 50 - 0,2 Δ b 1 ≥ 0.

Исходя из этих неравенств, найдем максимальное уменьшение и максима-льное увеличение первого ресурса.

Найдем максимальное уменьшение запаса сырья . Если запас первого ресурса уменьшается на величину Δ b 1 (Δ b 1<0), то выпуск первого продукта уменьшается на 0,6 Δ b 1, а выпуск второго продукта увеличивается на 0,2 Δ b 1. Отсюда следует, что максимальное уменьшение определяется значением Δ b 1, при котором план первого продукта будет равен 0:

x 1 = 100 + 0,6 Δ b 1 = 0, Δ b 1 = , .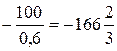

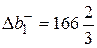Найдем максимальное увеличение запаса сырья . Если запас первого ресурса увеличивается на величину Δ b 1 (Δ b 1 > 0), то выпуск первого продукта увеличивается на величину 0,6 Δ b 1, а выпуск второго продукта уменьшается на 0,2 Δ b 1. Отсюда следует, что максимальное увеличение определяется значе-ниием Δ b 1, при котором план второго продукта будет равен 0:

x 2 = 50 - 0,2Δ b 1=0, .

Следовательно, нижняя граница интервала устойчивости

,

верхняя граница интервала устойчивости

.

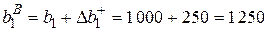Интервал устойчивости будет равен .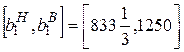

Пусть изменяется запас времени работы оборудования на величину Δ b 2

Для определения новых значений базисных переменных нужно к старым значениям этих переменных прибавить соответствующие значения столбца s 2, умноженные на Δ b 2: x 1= 100 - 20Δ b 2, x 2=50 + 10Δ b 2.

Так как теневая цена этого ресурса y 2 = 200, то выручка изменится на величину D Z = y 2 Δ b 2 = 200 Δ b 2.

Таким образом, при новом запасе сырья оптимальное решение прямой задачи X = { x 1=100 - 20Δ b 2, x 2=50 + 10Δ b 2, s 1=0, s 2 = 0}.

Выручка на этом плане составит Z = 9000+200Δ b 2.

Отсюда следует, что элементы столбца s 2 симплекс-таблицы показывают изменения базисных переменных x 1, x 2 и выручки Z при увеличении второго ресурса на 1: переменная x 1 уменьшается на 20, переменная x 2 увеличивается на 10 и выручка Z увеличивается на 200.

Поиск по сайту: