АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 6.1.3

Читайте также:
  1. I. 1.1. Пример разработки модели задачи технического контроля
  2. IV. ТИПОВОЙ ПРИМЕР РАСЧЕТОВ.
  3. X. примерный перечень вопросов к итоговой аттестации
  4. Б2. Пример №2
  5. Буду на работе с драконом примерно до 21:00.
  6. Булевы функции. Способы задания. Примеры.
  7. В нашем примере каждый доллар первоначального депозита обеспечил 5 дол. средств на банковских счетах.
  8. В некоторых странах, например в США, президента заменяет вице-
  9. В примере
  10. В странах Востока (на примере Индии и Китая)
  11. Вания. Одной из таких областей является, например, регулирова-
  12. Вариационные задачи с подвижными границами. Пример в теории управления.

Для мультипликативной функции

частные производные функции полезности положительны:

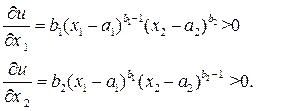(6.1.12)

при

Частные производные второго порядка

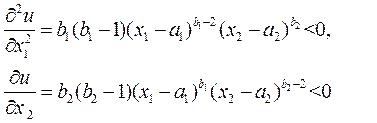(6.1.13)

отрицательны при b 1 < 1, b 2 < 1.Таким образом, для мультипликативной функ-ции свойства монотонности и строгой вогнутости выполняются.

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

 

1) Сформулируйте аксиомы отношения предпочтения.

2) Дайте определение функции полезности.

3) Как вычисляется предельная полезность товара?

4) В чем состоит экономический смысл предельной полезности товара?

5) В чем состоит экономический смысл свойства строгой вогнутости функции полезности?
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)