 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неоклассическая мультипликативная функция
Величина ai определяет минимальное количество приобретаемого товара. Набор (a1,a2) можно рассматривать как минимальную корзину потребления.
Нормальный товар, если выполняется неравенство 
, т.е. с ростом его цены спрос на него падает.
Однородность степени λ производственной функции означает, чтодля любого λ > 0 выполняется равенство
.
Оптимальный план x1, x2,…, xm допустимый план и на нем целевая функция достигает максимального значения.
Основная теорема двойственности: решение ЗЛП следует искать среди базисных решений и на оптимальных планах всегда выполняется равенство значений целевых функций.
Отношение предпочтения 
означает, что «набор товаров X предпочтительнее набора товаров Y».
Предельная норма замены первого товара вторым называют величину
.
Предельная норма замены S 12 показывает, на сколько единиц нужно уменьшить(увеличить) количество второго товарапри увеличении (уменьшении) первого товара на единицу, чтобы полезность осталась неизменной.
Предельная норма замены i –го ресурса j - м ресурсом равна
Предельная норма замены Rij показывает, на сколько единиц нужно уменьшить(увеличить) количество j -ого ресурса при увеличении (уменьшении) i -ого ресурса на единицу, чтобы выпуск остался неизменным.
Предельная полезностьтовара j равна частной производной 
от функции полезности.
Предельная производительность i -го ресурса равна частной производной 
от производственной функции.
Приведенная стоимость (приведенные издержки) производства продукции j разность междуудельными затратами zj и рыночной ценойнапродукцию j:
.
Производственная функция затраты-выпуск (функцию Леонтьева) задается формулой
.
Производство продукции j убыточное, если его приведенная стоимость 
,
- рентабельное, если его приведенная стоимость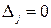 
;
- прибыльное, если его приведенная стоимость 
.
Производственной называется любая функция Y = f (x 1, x 2), которая каждому вектору затрат ресурсов X = (x 1, x 2)ставит в соответствиеколичество продукции Y, которое может быть получено при этих затратах.
Ресурс дефицитный, если он полностью используется в производстве.
Ресурс k ценный, если выполняется условие
Это означает, что повышение цены p на выпускаемую продукцию приводит к увеличению спроса на этот ресурс.
Ресурс k малоценный, если выполняется условие
Это означает, что повышение цены p на выпускаемую продукцию к уменьшению спроса на этот ресурс.
Ресурса k нормальным, если производная 
т.е. при возрастании цены на ресурс спрос на него падает.
Стандартная форма ЗЛП Найти переменные x 1, x 2 ,…, x n, которыемаксимизируют функцию
при ограничениях
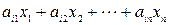
Симплекс-метод: алгебраический метод состоит в построении последовательности базисных решений прямой задачи, которая приводит к оптимальному базисному решению, если оно существует.
Ситуация равновесия или седловая точка матричной игры в чистых стратегиях: найтитакую ситуацию (i *, j *), в которой выигрыш игрока I удовлетворяет неравенствам
a (i, j *)≤ a (i *,j*) ≤ a (i *,j)
для всех чистых стратегий i,j обоих игроков. Число a (i *, j *) является выигрышем игрока I и называется значением или ценой игры.
Смешанная стратегия игрока I: любой упорядоченный набор из n чисел p= (p 1, p 2, …, p n), удовлетворяющий условиям
p 1 + p 2,+…+ p n=1, p i ≥ 0.
Число pi определяет вероятность, с которой игрок I выбирает строку i матрицы выигрышей.
Смешанная стратегия игрока II: любой упорядоченный набор из m чисел q= (q 1, q 2, …, qm), удовлетворяющий условиям
q 1 + q 2,+…+ q m=1, q j ≥ 0.
Число qj определяет вероятность, с которой игрок II выбирает столбец j матрицы выигрышей.
Ситуация равновесия матричной игры в смешанных стратегиях:
для пары стратегий (p *, q *) выполняется неравенство 
для любых смешанных стратегий игроков p, q. В этом случае пару стратегий (p *, q *) называют ситуацией равновесия матричной игры, а число v*=V(p*, q*) – значением матричной игры.
Cпрос потребителя или точка локального рыночного равновесия – оптимальное решение 
задачи потребительского выбора.
Теневые цены соответствующие данному базисному решению: все ограничения двойственной задачи, соответствующие базисным переменным xj, заменяются равенствами
,
решение y1, y2, …,ym полученной системы определяет теневые цены, соответст-вующие данному базисному решению.
Теорема об оценке: при изменении запаса ресурса на Δ b выручка изменится на величину D Z=y Δ b.
Товар – некоторая услуга, поступающая в продажу в определенное время и в определенном месте.
Товар Гиффина, если с ростом его цены спрос на него растет, т.е.
Товар Гиффина – это популярный товар, который продается по слишком низкой цене. Это вызывает сомнение в его качестве, что приводит к низкому спросу на него. Поднятие цены может повысить спрос на него.
Транспортная задача: в задаче требуется найти план перевозок { xij }, который минимизирует транспортные расходы
при ограничениях
, 
, x ij ≥ 0
Поиск по сайту: