АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Модель Стоуна. Пусть полезность потребителя описывает неоклассическая мультиплика-тивная функция

Читайте также:
  1. V2. Модель IS-LM
  2. V2. Равновесие совокупного спроса и предложения. Модель AD-AS.
  3. V2: Равновесие совокупного спроса и предложения. Модель AD-AS.
  4. XXII. Модель «К» и отчаянный риск
  5. А) Модель Хофстида
  6. А-модель
  7. Адаптивная модель
  8. Адаптивная полиномиальная модель первого порядка
  9. Аксилераторно-мультипликаторная модель (модель Самуэльсона-Хикса).
  10. Акцептор действия — механизм, предвосхищаяющий закодированную модель будущего.
  11. Альтернативні моделі розвитку. Центральна проблема (ринок і КАС). Азіатські моделі. Європейська модель. Американська модель
  12. Альтернативные модели потребления: модель межвременного выбора И. Фишера, теория перманентного дохода М. Фридмена, гипотеза жизненного цикла Ф. Модильяни

Пусть полезность потребителя описывает неоклассическая мультиплика-тивная функция

.

Величина ai определяет минимальное количество i – го товара, а величина bi – коэффициент эластичностиэтого товара. Набор (a 1, a 2) можно рассматривать как минимальную корзину потребления.

Модель Стоуна можно сформулировать как оптимизационную задачу:

найти такой потребительский набор, в котором достигается максимум функции полезности

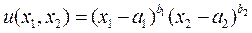
при ограничениях

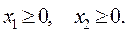
Решая полученную задачу нелинейного программирования, получаем формулы для функций спроса


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)