АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение. 1. Найдем полезностьнабор X1 = (2,4):

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. I.5.4. Решение задачи линейного программирования
  3. II этап: Решение задачи на ЭВМ в среде MS Excel
  4. II этап: Решение задачи на ЭВМ в среде MS Excel
  5. II этап: Решение задачи на ЭВМ в среде MS Excel
  6. II этап: Решение задачи на ЭВМ средствами пакета Excel
  7. II. Решение логических задач табличным способом
  8. II.1.3. Решение транспортной задачи в QSB
  9. III. Разрешение споров в международных организациях.
  10. III. Решение логических задач с помощью рассуждений
  11. IV. Воскрешение мертвых
  12. MatLab: решение дифференциальных уравнений

1. Найдем полезностьнабор X 1 = (2,4):

.

Кривая безразличия

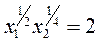
определяет все наборы товаров, которые имеют такую же полезность как набор X1= (2,4). Из этого уравнения можно найти набор товаров, в котором количества второго товара равно x 2 = 1, подставив это значение в уравнение кривой безразличия

, x 1=4.

Таким образом, наборы X1= (2,4), X2= (4,1) безразличны для потребителя.

2. Найдем частные производные функции полезности

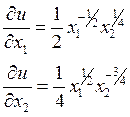
Предельная полезность первого товара в наборе X1= (2,4) равна значению частной производной

 

 

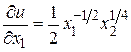
в точке (2,4):

.

Предельная полезность второго товара в наборе X 1 = (2,4) равна значению частной производной

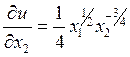
в точке (2,4):

.

Найдем изменение полезности, если количество первого товара увеличивается на 0,1, т.е. Δ x 1 = 0,1, а количество второго товара уменьшается 0,2, т.е. Δ x2 = -0,2. Приближенное изменение полезности вычислим по формуле

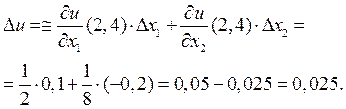
Следовательно, полезность набора X 1 = (2,4), равная 2, увеличится на 0,025. Таким образом, полезность нового набора X3 = (2,1, 3,8) составит 2,025.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)