Раздел 4. Целочисленное и нелинейное программирование

4.1. Задача о назначениях

Изучаемые вопросы:

· Формулировка задачи о назначениях;

· Реализация задачи о назначениях в Excel.

В целочисленном линейном программировании все или часть переменных должны принимать целые значения. В качестве примера рассмотрим задачу о назначениях.

Предположим, что n работников необходимо назначить на n работ. Обозначим через cij стоимость выполнения работником i работы j. Требуется найти оптимальное распределение работников по всем работам. Заметим, что число работников и число работ одинаково. Поэтому каждый работник может быть назначен только на одну работу. Обозначим через x ij переменную, которая принимает значение 1,если работник i назначен на работу j и 0 – в противном случае. Тогда ограничение

означает, что каждый работник может быть назначен только на одну работу.

Аналогично, ограничение

означает, что каждая работа может быть выполнена только одним работником.

Стоимость выполнения всех работ будет определяться целевой функцией

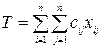
Таким образом, математически задача о назначениях состоит в определении переменных xij, которые минимизируют стоимость выполнения всех работ

при ограничениях

,

,

xij принимает значения 0 и 1.

Задача о назначениях является частным случаем транспортной задачи, в которой работники – пункты отправления, а работы – пункты назначения. Объемы производства и потребления равны 1, а стоимость перевозки равна стоимости выполнения работы. Поэтому задачу о назначениях можно решить в Поиске решения.

Пример 4.1.1

Рассмотрим задачу о назначении четырех работников на четыре работы. Стоимость выполнения всех работ задает матрица

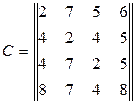
Решение задачи о назначениях означает определение матрицы назначений

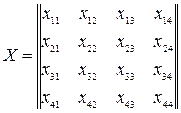
Переменная x_ij принимает значение 1,если работник i назначен на работу j и 0 – в противном случае.

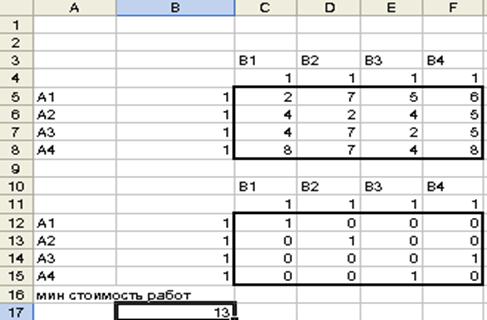
Для решения задачи в Excel можно использовать электронные таблицы, составленные для решения транспортной задачи (табл. 4.1.1).

Таблица 4.1.1

1) Внесение исходных данных

В ячейках C5:F8 поместим значения матрицы стоимостей C. В ячейки C4:F4 и B5:B8 внесем 1 (правые части ограничений). Значения в изменяемых ячейках C12:F15 будут определять матрицу назначений X.

формулы для матрицы назначений как показано ниже.

2) Внесение формул.

В ячейки B12:B15 внести формулы для суммы строк матрицы Х. В ячейки C11: F11 внести формулы для суммы столбцов матрицы Х. В целевую ячейку B17 внести формулу для вычисления целевой функции Z.

3) Заполнить окна Поиска решения (рис. 4.1.1) и (рис. 4.1.2)

4) В результате получим оптимальное решение (табл. 4.1.2).

Оптимальное решение задачи о назначениях состоит:

в назначении первого работника на первую работу,

в назначении второго работника на вторую работу,

в назначении третьего работника на четвертую работу,

в назначении четвертого работника на третью работу.

Стоимость работ составит 13.

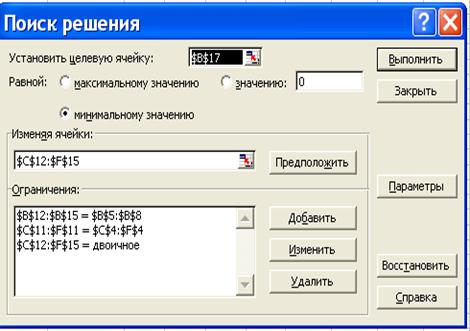
Рис. 4.1.1

Рис. 4.1.2

Вопросы для самопроверки

1. Может ли быть переменная равна 2 в задаче о назначениях?

2. В чем смысл ограничений задачи о назначениях?

3. Объяснить смысл ограничений

4. Объяснить смысл ограничений

Таблица 4.1.2

4.2. Нелинейное программирование

Изучаемые вопросы:

· Формулировка общей задачи нелинейного программирования;

· Реализация задачи квадратичного программирования в Excel.

В дифференциальном исчислении рассматриваются необходимые и достаточные условия экстремума функций нескольких переменных. Для решения задач при наличии ограничений в виде равенств используется метод Лагранжа.

В нелинейном программировании рассматриваются задачи на экстремум с ограничениями в виде неравенств. В общей постановке задача нелинейного программирования состоит в определении точек максимума или минимума функции нескольких переменных

max (min) f (x 1, x 2,…, xn) (4.2.1)

при ограничениях

g i (x 1, x 2,…, x n) ≤ 0, i = 1, 2,…, m 1,

g i (x 1, x 2,…, x n) ≥ 0, i = m 1+ 1, m 1 + 2,…, m 2, (4.2.2)

g i (x 1, x 2,…, x n) = 0, i = m 2+ 1, m 2+2,…, m.

Множество (x 1, x 2,…, xn), для которых выполнены все ограничения (4.2.2) называется областью допустимых решений. Функция f (x 1, x 2,…, xn) называется целевой функцией.

Для определения необходимых условий существования решения этой задачи используются условия Куна-Таккера. Эти условия являются достаточными, если область допустимых решений выпуклое множество, целевая функция вогнутая (выпуклая).

Рассмотрим задачу квадратичного программирования.

Введем матричные обозначения

X = (x 1, x 2,…, x n) ^T,

C = (c 1, c 2,…, c n),

B = (b 1, b 2,…, b n) ^T,

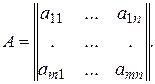
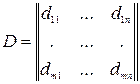
Задача квадратичного программирования состоит в определении вектора X, который доставляет максимум (минимум) целевой функции Z = C X + X^T D X

при ограничениях AX ≤ B, X ≥ 0.

Если матрица D – симметрическая и положительно определенная, то целевая функция будет строго выпуклой по X в задаче минимизации. Если матрица D – симметрическая и отрицательно определенная, то целевая функция будет строго вогнутой по X в задаче максимизации. Из линейности ограничений следует, что область допустимых решений – выпуклая. Условия Куна-Таккера для задачи квадратичного программирования являются необходимыми и достаточными. Реализация этих условий сводится к решению некоторой системы линейных уравнений. Для решения этой системы можно использовать режим Поиск решения в программе Excel.

Пример 4.2.1

Рассмотрим задачу квадратичного программирования. Найти минимум целевой функции

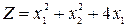(4.2.3)

при ограничениях

x 1 + x 2 ≥ 200, x 1 ≥ 0, x 2 ≥ 0 (4.2.4)

В матричных обозначениях

X = (x 1, x 2) ^T,

C = (4,0),

B = (-200),

A = (-1,-1), .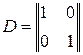

Поиск по сайту: