 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства функции полезности
1. Свойство монотонности.Предельная полезностьтовара
Функция полезности удовлетворяет свойству монотонности, если из неравенств
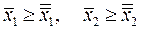
следует
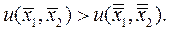 (6.1.5)
(6.1.5)
Пусть функция полезности u (x 1, x 2) дифференцируема. В этом случае свойс-тво монотонности означает, что частные производные функции полезности положительны:
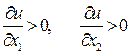 . (6.1.6)
. (6.1.6)
Свойство монотонности означает, что рост потребления хотя бы одного товара приводит к увеличению полезности u (x 1, x 2)всего набора товаров. Частная производная 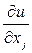 называется предельной полезностью товара j. Предельная полезность товара измеряется в ед. полезности за ед. товара (в ед. полезн./ед. товара).
называется предельной полезностью товара j. Предельная полезность товара измеряется в ед. полезности за ед. товара (в ед. полезн./ед. товара).
Пусть потребления товара 1 изменяется на величину 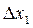 , а потреблении товара 2 – на величину
, а потреблении товара 2 – на величину 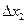 . Тогда величина
. Тогда величина
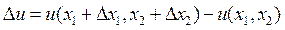
определяет приращение полезности при замене набора (x 1, x 2) на набор 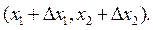 Приращение полезности можно приблизительно вычислить по формуле
Приращение полезности можно приблизительно вычислить по формуле
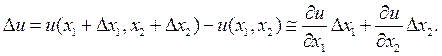 (6.1.7)
(6.1.7)
В частности, если потребления товара 1 изменяется на величину 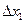 , а потреблении товара 2 не изменяется
, а потреблении товара 2 не изменяется 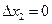 , то
, то
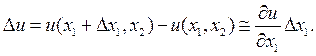 , (6.1.8)
, (6.1.8)
если потребления товара 1 не изменяется 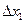 = 0, а потребление товара 2 изменяется на величину
= 0, а потребление товара 2 изменяется на величину 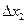 , то
, то
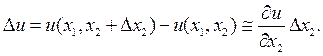 (6.1.9)
(6.1.9)
Поиск по сайту: