 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Раздел 2. Решение прямой задачи линейного программирования симплекс-методом
При изучении данного раздела Вам предстоит:
1) Изучить четыре темы:
a. Алгоритм симплекс-метода;
b. Анализ симплекс-таблиц;
c. Интервалы устойчивости. Ценность ресурсов;
2) Ответить на вопросы рубежного теста к разделу 2.
Если Вы будете испытывать затруднения в ответах, обратитесь к Учебному пособию (Глава 2) или к Глоссарию – краткому словарю основных терминов и положений.
2.1. Теоремы двойственности. Алгоритм симплекс-метода
Изучаемые вопросы:
· Теорема равновесия и следствия из нее;
· Критерий оптимальности и свойства оптимального плана;
· Общая схема симплекс-метода;
· Решение примера;
· Алгоритм симплекс-метода на примере задачи распределения ресурсов.
· Анализ оптимальной симплекс-таблицы
В линейном программировании доказываются две теоремы двойственности.
Теорема 1 (основная теорема двойственности). Пусть xj, j = 1, 2,…, n обозначает допустимый план прямой задачи, а yi, i = 1, 2,…, m – допустимый план двойственной задачи. Тогда выполняется неравенство:
 , (2.1.1)
, (2.1.1)
при этом на оптимальных планах всегда выполняется равенство. Если хотя бы одна из задач не имеет допустимого плана, то ни одна из них не имеет оптимального решения.
Из теоремы 1 следует, что решение задачи линейного программирования следует искать среди базисных решений.
Теорема 2 (теорема равновесия). Для того чтобы допустимые планы 
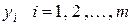 прямой и двойственной задач были оптималь-ными, необходимо и достаточно, чтобы выполнялись равенства
прямой и двойственной задач были оптималь-ными, необходимо и достаточно, чтобы выполнялись равенства

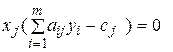 (2.1.2)
(2.1.2)
Следствия:
1) Если для некоторого ограничения прямой задачи в стандартной форме выполняется строгое неравенство
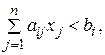 (2.1.3)
(2.1.3)
то значение двойственной переменной, соответствующей этому ограничению yi = 0, т.е. теневая цена недефицитного ресурса равна 0.
2) Если оптимальное значение базисной переменной x j> 0, то
 , (2.1.4)
, (2.1.4)
т.е. производство данной продукции рентабельно.
Определим критерий, по которому можно определить является ли допустимое базисное решение оптимальным.
Критерий оптимальности. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций Z = W, то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно.
Заметим, что критерию оптимальности удовлетворяет базисное решение прямой задачи в примере 1.3.1, п.2.
x 1 = 100, x 2 = 50, s 1=0, s 2=0 и соответствующее ему решение двойственной задачи y 1 =4, y 2 = 200 является допустимым.
Из теорем двойственности следует, что оптимальные решения прямой и двойственной задач распределения ресурсов должны удовлетворять следующим свойствам:
1) все производства, входящие в оптимальный план прямой задачи должны быть рентабельными, т.е. для всех базисных переменных xj приведенные стоимости Δ j = 0;
2) все производства, не входящие в оптимальный план, должны быть неприбыльными; т.е. для всех небазисных переменных xj приведенные стоимости Δ j ≥ 0;
Иначе говоря, допустимый базисный план прямой задачи X – неоп-тимальный, если хотя бы для одной небазисной переменной xj величина Δ j < 0, т.е. хотя бы одно небазисное производство прибыльно.
3) максимальное значение выручки в прямой задаче Z будет равно минимальной стоимости всех ресурсов в теневых ценах W, т.е. max Z = min W.
Симплекс-метод состоит в построении последовательности базисных решений прямой задачи, которая приводит к оптимальному базисному решению. Выбирают некоторым способом начальный базисный план прямой задачи и находят теневые цены, ему соответствующие. Если в этих ценах все производства – неприбыльные, т.е. теневые цены являются допустимыми, то начальный базисный план прямой задачи является оптимальным планом. Если же в этих ценах хотя бы одно небазисное производство прибыльно, то переменная одного прибыльного производства вводится в базисный план и для нового базисного плана повторяется все, что и для начального базисного плана прямой задачи. Так продолжается до тех пор, пока не будут найдены такие теневые цены, при которых все производства будут неприбыльными. Алгоритм симплекс-метода покажем на примере.
Пример 2.1.1
Построение начального базисного плана. Найдем оптимальный план выпуска продукции для примера 1.1.1. Запишем каноническую форму задачи:
 (1.1.10)
(1.1.10)
при ограничениях
 , (1.1.11)
, (1.1.11)
 , (1.1.12)
, (1.1.12)
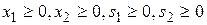 . (1.1.13)
. (1.1.13)
Пусть x 1, x 2 – свободные переменные (т.е. x 1= x 2=0). Тогда базисные переменные s 1 =1000 и s 2=25. Двойственные переменные, соответствующие этому плану, будут равны y 1 =0, y 2 =0, а величины:
D1 = 5 y 1 + 0,1 y 2 - 40= -40,
D2 = 10 y 1 + 0,3 y 2 -100 = -100 (см. пример 1.3.1 п.1).
В симплекс-методе удобно использовать симплекс-таблицы. Рассмотрим построение первой симплекс-таблицы для выбранного начального базисного решения (табл.2.1.1). В первом столбце симплекс-таблицы поместим обозначения базисных переменных s 1 и s 2, а во втором – их числовые значения 1 000 и 25. Остальные столбцы состоят из коэффициентов перед переменными x j в левых частях ограничений (1.1.11), (1.1.12). Последняя строка симплекс-таблицы состоит из значения целевой функции Z = 0 и величин y 1 = 0, y 2 = 0, Δ1 = -40, Δ2 = -100.
Таблица 2.1.1
| Базис | Значение | x 1 | x 2 | s 1 | s 2 |
| s 1 | |||||
| s 2 | 0,1 | 0,3 | |||
| z | -40 | -100 | |||
| Δ1 | Δ2 | y 1 | y 2 |
Переход от одного базисного плана к другому сопровождается преобразованием симплексных таблиц. Такой переход называется итерацией. Каждая итерация состоит из нескольких действий.
Поиск по сайту: