 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Найти оптимальное решение двойственной задачи
Из первого задания следует, что допустимое базисное решение
X * = { x 1 = 0, x 2 = 83  , s 1 = 166
, s 1 = 166 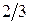 , s 2 = 0}
, s 2 = 0}
является оптимальным решением прямой задачи.
По оптимальному базисному решению X* прямой задачинайдем оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным x 2, s 1, нужно заменить равенствами
x 1  5 y 1+ 0,1 y 2
5 y 1+ 0,1 y 2 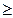 40,
40,
x 2  10 y 1+ 0,3 y 2 =130,
10 y 1+ 0,3 y 2 =130,
s 1  y 1 = 0,
y 1 = 0,
s 2 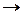 y 2
y 2 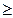 0.
0.
Из этих равенств найдем оптимальные значения двойственных переменных

Минимальное значение целевой функции равно
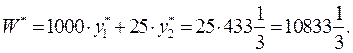
Оптимальная теневая цена 1 кг сырья равна 0, а оптимальная теневая цена 1 часа работы оборудования равна 
Стоимость ресурсов, затраченных на изготовление единицы продукции 1, равна

а стоимость ресурсов, затраченных на изготовление единицы продукции 2, равна

Приведенные стоимости каждого видапродукции будут равны
 ,
,
 .
.
Отсюда следует, что производство единицы продукции 1 принесет убыток  а производство единицы продукции 2 – рентабельно (
а производство единицы продукции 2 – рентабельно ( ).
).
Определим целесообразность производства продукции 3, для которой на единицу продукции требуется 4 кг. сырья и 0,4 часа времени изготовления. Рыночная цена составляет 120 у.е. за единицу продукции. Для этого вычислим стоимость ресурсов, затраченных на изготовление единицы продукции 3:

Приведенная стоимость этого видапродукции будет равна

Отсюда следует, что производство единицы продукции 3 принесет убыток 
Поиск по сайту: